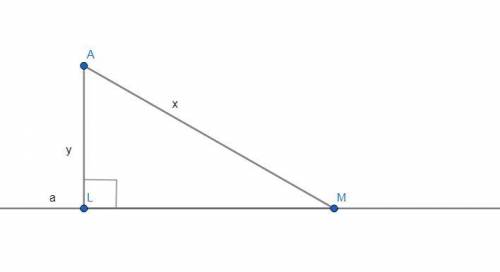
Чертёж смотрите во вложении.
Дано:
а - прямая.
АL - перпендикуляр от точки А до прямой а.
АМ - наклонная от точки А до прямой а.
∠ALM = 90°.
АМ+AL = 11 см.
Разность длин наклонной и перпендикуляра = 1 см.
Найти:
Расстояние от точки А до прямой а = ?
О каком расстоянии идёт речь в задании? Дело в том, что расстояние от точки до прямой - длина перпендикуляра, проведённого из этой точки к этой прямой. Поэтому, мы будем искать длину перпендикуляра AL.Так как АМ - наклонная, то она больше перпендикуляра AL (это не сложно доказать, если рассмотреть получившиеся прямоугольный ΔALM). Итак, поэтому, AM-AL = 1 см.Введём переменные. Пусть АМ = х, а AL = y. Составим систему линейных уравнений и решим её методом подстановки -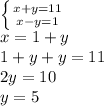
AL = y = 5 см.ответ: 5 см.
1. Угол между наклонной к плоскости и плоскостью - это угол между наклонной и ее проекцией на плоскость. Искомый угол - угол МАО. Высота правильного треугольника равна h=(√3/2)*a = (√3/2)*2√3=3. АО=(1/3)*h = 1 (свойство медианы). Tg(<MAO) = MO/AO = √3.
ответ: α = arctg√3 = 60°
2. Искомый угол - угол между наклонной и ее проекцией, то есть угол АВК. Sin(<ABK) = KA/KB = AC*tg60/5 = 5√3/11. <ABK = arcsin(0,787) ≈ 51,9°.
3. Опустим перпендикуляры SP и SH из точки S к сторонам АВ и АD соответственно. Прямоугольные треугольники APS и AHS равны по гипотенузе и острому углу. Значит АР=АН и АРОН - квадрат. тогда АО = АН*√2 (диагональ квадрата), АS = 2*АН (в треугольнике ASH катет АН лежит против угла 30°, а AS - гипотенуза). Косинус искомого угла (между наклонной AS и плоскостью АВСD, равного отношению проекции наклонной к наклонной) = АО/AS = АН√2/(2*АН) = √2/2.
ответ: искомый угол равен 45°.
S=32√2 см^2
Объяснение:
ABCD - ромб
1. пусть х( х>0) - коэффициент пропорциональности,
<А=1х, <В=3х
<А+<В=180° (сумма углов при одной стороне ромба равна 180°)
уравнение:
1х+3х=180°
4х=180°
х=45°
2. S ромба =а×а×sin a, a - угол между сторонами ромба
a= 8 см
S=8×8×sin 45°=64×(√2/2)=32√2