Углы 3 и 2 - вертикальные. Поэтому, ∠3 = ∠2 = 112°.
За счёт того, что m║n, то ∠2 = ∠1 = 112° как соответственные.
ответ: 112°.
Площадь правильного шестиугольника
S1 =3√3/2 a^2
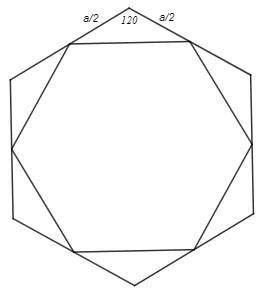
Построим первый внутренний шестиугольник.
Его стороны отсекают 6 равных треугольников, найдем их суммарную площадь.
6 S△ =6 *1/2 (a/2)^2 sin120 =3√3/8 a^2
Видим, что площадь шести треугольников равна 1/4 площади исходного шестиугольника.
Тогда площадь внутреннего шестиугольника равна 3/4 площади исходного.
И так далее.
Имеем бесконечно убывающую геометрическую прогрессию, знаменатель q=3/4.
Первый член b1=3√3/2 (площадь правильного шестиугольника со стороной 1)
Сумма членов бесконечно убывающей геометрической прогрессии
S =b1/(1-q) =3√3/2 : 1/4 =6√3
Итоговая контрольная работа(Решите хотя бы три)
1. Основание конуса совпадает с одним из оснований цилиндра, а вершина конуса с центром
другого основания цилиндра. Во сколько раз площадь осевого сечения цилиндра больше
площади осевого сечения конуса?
2. Все рёбра треугольной пирамиды равны 1. Рассмотрите сечение этой пирамиды плоскостью,
параллельной двум противоположным (скрещивающимся) рёбрам пирамиды. Как называется
многоугольник, получившийся в сечении? Чему равен его периметр? В каких пределах
меняется его площадь?
3. Найдите радиус шара, касающегося трёх граней единичного куба и вписанного в этот куб
шара.
4. Отрезок, длина которого равна 1, образует угол в 45° с одной из гранью прямого двугранного
угла, и он же образует угол в 30° с другой гранью этого же двугранного угла. Найдите длину
проекции этого отрезка на ребро двугранного угла.
5. Высота пирамиды равна 1, все двугранные углы при основании равны 45°, периметр
многоугольника, расположенного в основании, равен 2р. Найдите площадь этого
многоугольника. При каких р такая пирамида возможна?
6. В основании треугольной пирамиды АВСD лежит правильный треугольник АВС. Найдите его
стороны, если известно, что все боковые грани этой пирамиды равновелики и ВD = СD = 1,
АD = 2
Объяснение:
ответ: 112.
За властивістю двох паралельних прямих і січної, кути 1 та 2 - відповідні (тому вони рівні), а кути 3 та 2 - вертикальні (тому вони також рівні). Таким чином кути 3 та 1 - однакові.