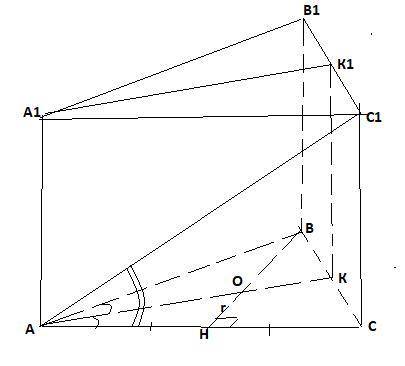
" Основой прямой призмы является равнобедренный треугольник с углом a при основании и радиусом вписанной окружности r. Диагональ боковой грани, проходящей через основание равнобедренного треугольника, наклонена к плоскости основания под углом y . Отметьте, какие из приведенных четырех утверждений правильные
1. Плоскость, проходящая через боковое ребро призмы и уентр круга, вписанного в основание, делит двугранный угол при боковом ребре призмы пополам
2. Боковое ребро призмы равна 2r*ctg*a/2*tgy
3. Одна из сторон основания призмы равна r*ctg*a/2
4. Один из двугранных углов при боковом ребре призмы равна a"
Объяснение:
1) Т.к. центр вписанной окружности лежит в точке пересечения биссектрис, то плоскостью, проходящей через боковое ребро призмы и центр круга, вписанного в основание, будет плоскость АКК₁А₁ , где АК, А₁К₁-биссектрисы нижнего и верхнего оснований.
Поэтому 1 утверждение верное.
2) Боковое ребро найдем из ΔАСС₁ -прямоугольного : СС₁=АС*tgy.
АС найдем из ΔАОН :
ΔАВС-равнобедренный. В равнобедренном
треугольнике биссектриса ВН является высотой и
медианой .АК-биссектриса, значит ∠ОАН=α/2 .
АН= r /(tgα/2 ) , 2АН=АС= =2r*ctg α/2 .
Получаем СС₁=2r*ctg α/2 *tgy.
Поэтому 2 утверждение верное.
3) 3 утверждение неверное , т.к. в п 2 найдена сторона основания АС=2r*ctg α/2 . а боковая сторона будет искаться через косинус или синус ΔАВН.
4)4 утверждение верное . Это двугранный угол , например САА₁В, т.к
АА₁⊥АС и АА₁⊥АВ и ∠ВАС=α
Lo=12,6π;. P∆=18,9√3;. S∆=29,7675
Объяснение:
Дано: ∆АВС-правильный,
R=6,3
Lo=?;. P∆=?;. S∆=?.
Решение: центр окружности лежит на пересечении медиан ∆, они же высоты и биссектрисы этого ∆, =>
а-сторона ∆, h=а√3/2; R=2/3*h
(медиана делится точкой пересечения в соотношении 2:1, считая от вершины,
h=3R/2;. 3R/2=a√3/2;. a=3R/√3
a=√3R
Lo=2πR;. Lo=2π*6,3=12,6π
P∆=3a=3√3R;. P∆=3√3*6,3=18,9√3
S∆=1/2*a^2*Sin60=1/2*√3/2*a^2=√3/4a^2=√3/4(√3R)^2=3√3/4*R^2
S∆=3√3/4*6,3^2=29,7675=
=29, 307/400 запись целая часть, числитель/знаменатель