22√7
Объяснение:
Формула для нахождения площади трапеции через ее основания и высоту:
S =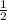 
* (a + b) * h, где a, b — основания трапеции, h — высота трапеции.
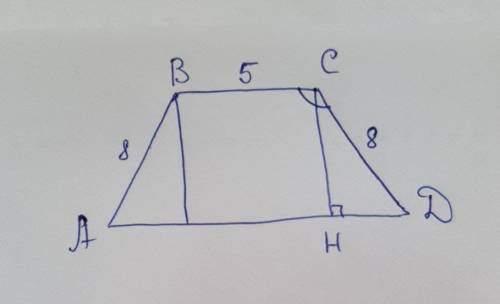
СН ⊥ АД, СН - высота трапеции.
Рассмотрим ΔСДН(∠Н=90°).
СН = sin ∠Д * СД,
НД = cos ∠Д * СД.
Воспользуемся формулами приведения:
соsC = соs( 180°-∠Д) = - соs ∠Д ⇒ соs ∠Д = - соsC = 3/4
sin² ∠Д = 1 - соs² ∠Д = 1 - 9/16 = 7/16
sin ∠Д = 
= √7 / 4
СН = (√7 / 4 )* 8 = 2√7
НД = 3/4 * 8 = 6
т.к. трапеция АВСД - равнобокая, то АД = ВС+2*НД = 5+2*6=17 см
S = 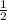* (5+17)* 2√7 = 22√7
Есть 2 вариант.
После того, как нашли НД, через cos ∠Д, воспользоваться т. Пифагора и найти СН из ΔСДН :
СН² = СД²-НД² = 64-36 = 28
СН = √28= 2√7
Дано: Прямі a та b — паралельні, пряма c — січна, кути ∠1 і ∠6 — внутрішні односторонні, ∠1:∠6 = 4:5. Знайти градусні міри ∠1 та ∠7, ∠4 та ∠6.
Рішення:
Нехай кут ∠1 = 4х°, тоді кут ∠6 = 5х°. Сума внутрішніх односторонніх кутів рівна 180°. Складемо і вирішимо мат. модель:
∠1 = 4х° = 4·20 = 80°
∠6 = 5х° = 5·20 = 100°
Визначимо внутрішні різносторонні (навхрест лежачі) кути:
∠1 = ∠7 = 80°
∠6 = ∠4 = 100°
Відповідь: градусна міра внутрішніх різносторонніх кутів — 80° та 100° відповідно.