а) Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено условие: боковые ребра пирамиды равны.
Длины сторон
AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 6 0 0 36 6
BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²) = -3 5,19615 0 36 6
CD = √((xD-xC)²+(yD-yC)²+(zD-zC)²) = 0 -3,46410 2 16 4
AD = √((xD-xA)²+(yD-yA)²+(zD-zA)² = 3 1,73205 2 16 4
AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²) = 3 5,19615 0 36 6
BD = √((xD-xB)²+(yD-yB)²+(zD-zB)²) = -3 1,73205 2 16 4 .
Как видим, в основании правильный треугольник и все боковые рёбра равны. Значит, пирамида правильная.
б) Основание апофемы пирамиды,лежащей в грани DAC, это середина стороны основания АС - точка Е.
Даны точки A(-1;0;1), C(2;3√3;1)
Е = ((-1+2)/2); (0+3√3)/2); ((1+1)/2)) =((-1/2); (3√3/2); 1).
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ = ?
= ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда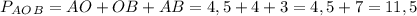 см
см