5,2 см и 9,6 см²
Объяснение:
Расстояния - это перпендикуляры. Проводя из точки пересечения диагоналей перпендикуляры к сторонам, получаем, что половина диагонали, заключенная между этими перпендикулярами, является диагональю в маленьком(зеленом) прямоугольнике, образованном ими, т.е. по т. Пифагора она равна √(1²+2,4²)=2,6 см. Вся диагональ в два раза больше, т.е. она равна 5,2 см.
Большой прямоугольник в свою очередь можно разбить на 4 маленьких, образованных перпендикулярами, проведенными из точки пересечения диагоналей. Т.е. его площадь в четыре раза больше, чем площадь одного маленького. Площадь маленького равна 1×2,4=2,4 см², тогда площадь исходного прямоугольника равна 2,4×4=9,6 см²
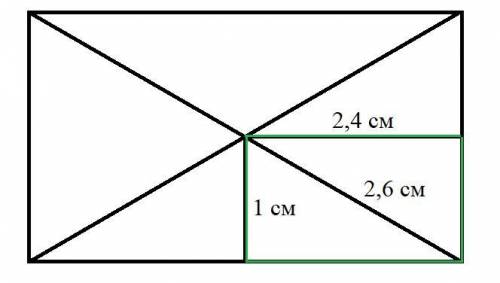
См. рис.
Так как AD - диаметр окружности, то угол ∠ABD = 90°
Следовательно, оставшийся угол прямоугольного
треугольника ΔABD: ∠BAD = 90 - 65 = 25°
Так как угол ∠BAD - вписанный, то величина дуги, на которую он опирается:
∪BCD = 2 · ∠BAD = 50°
Искомый угол ∠С = ∠BCD опирается на оставшуюся дугу
окружности:
∪BAD = 360 - ∪BCD = 360 - 50 = 310°
И величина угла ∠С = 310 : 2 = 155°
Причем, величина угла ∠С не зависит от местоположения точки С на дуге ∪BCD, так как в любом случае этот угол опирается на дугу ∪BAD, равную 310°