Точку A соединяем с точкой C, т.к. они лежат в одной плоскости.
Через точки A и B, лежащие в одной плоскости проводим прямую до пересечения со стороной DK или DN.
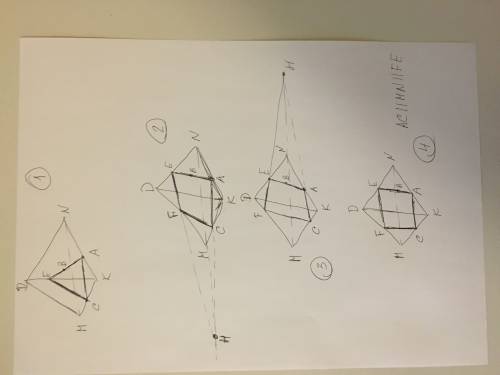
1. Предположим, что прямая AB пересекла сторону DK в точке E. Тогда просто соединяем точки E и C и получаем в сечении треугольник AEC.
2. Предположим, что прямая AB пересекла сторону DN в точке E. Тогда продолжим отрезок AC до пересечения с прямой MN (если они не параллельны) в точке H (см. рис 2 и 3). Точку H соединяем с точкой E, получая пересечение с ребром DM в точке F. Окончательно соединяем точку F с C и получаем в сечении четырехугольник AEFC.
Если AC || MN, то через точку E в плоскости MDN проводим прямую параллельную MN до пересечения с ребром MD в точке F. Окончательно соединяем точку F с C и получаем в сечении четырехугольник AEFC.
Р=12+18+20=50см
ответ 50
опустим из вершины с на ад перпендикуляр: Δаве=Δдск⇒
АЕ=ДК=(17-5)/2=6
ответ 6
∠САД=∠АСВ=28° как внутренние накрестлежащие
в Δавс ∠ВАС=АСВ=28° как углы при основании равнобедренногоΔ
∠ВАД=∠СДА∠ВАС+∠АСВ=28+28=56° как углы при основании равнобедренной трапеции
∠АВС=∠ВСД=(360-2*56)/2=(360-112)/2=248/2=124°
ответ 59°,59°,124°,124°
пусть ВС =х, тогда АД =х+6 Сред линяя равна
МК=(х+х+6)/2, а по условию 7см
составим и решим уравнение
2х+6 / 2=7
2х+6=7*2
2х=14-6
х=8/2
х=4, значит вс=4, тогла ад=10
ΔАСД и ΔАСК подобны(т.к СК=1/2СД ∠С общий ∠СКО=∠СДА)⇒СО=1/2СА
т.е ОК - средняя линия ΔАСД⇒ ОК=1/2АД=1/2*10=5
МО=МК-ОК=7-5=2
ответ 5 и 2
ΔАВС и КВМ подобны(тк ∠В - общий, КВ=1/3АВ, МВ=1/3СВ)
⇒КМ=1/3АС=1/3*9=3см
ΔАВС и ОВN подобны(тк ∠В - общий,OВ=2/3АВ, NВ=2/3СВ)
⇒ON=2/3АС=2/3*9=6см
ответ 3 и 6