Нарисуй параллелограмм, прямую и все пересекающиеся точки. Выдели каким-нибудь контрасным цветом треугольники ABE и EFC.
Из рисунка станет ясно, что угол BEA равен углу FEC, так как это вертикальные углы,
а угол ABE равен углу FCE как накрест лежащие, получившиеся при пересечении двух параллельных прямых AB и DF третьей прямой BC (у параллелограмма противоположные стороны параллельны).
Вот и все. Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
Отрезок BM — медиана равнобедренного треугольника ABC (AB=BC). На стороне AB отметили точку К такую, что КМ параллельно BC. Докажите, что BK=КМ.
Дано :
AB = BC (боковые стороны)
AM = MC ( BM медиана)
КМ || BC ( К ∈ [AB] )
- - - - - - -
Док- ать BK = KM
Объяснение:
AM = MC и КМ || BC ⇒ (т. Фалеса ) AK = BK = AB/2 = BC/2
следовательно КM средняя линия треугольника ABC
КM = BC/ 2 но и BK = BC / 2 ⇒ BK = KM ч.т.д.
Можно и по другому (2 -ой В прямоугольном треугольнике AMB (∠AMB =90° , AB _гипотенуза медиана BM треугольника ABC одновременно и высота ) медиана MK = AB/2 (половине гипотенузы) = BK.
рис. cм ПРИЛОЖЕНИЕ
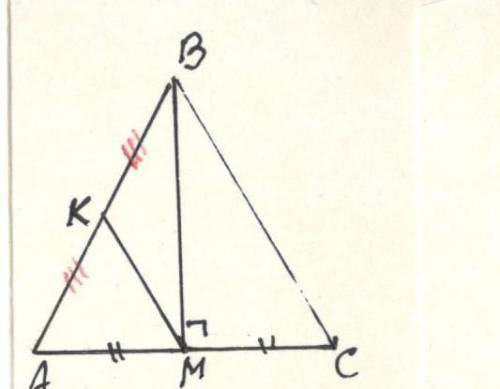
МЬЯВП
Объяснение: