NВ = 6√17, или NВ ≈ 24,74 см
Объяснение:
Задача № 4.
1) С1С = 6 см, а как сумма С1М и МС, выраженная в частях:
1 + 2 = 3 части; следовательно 1 часть = 6 : 3 = 2 см.
Откуда С1М = 1 * 2 = 2 см, а МС = 2*2 = 4 см.
2) Согласно условию, D1К = КD. Следовательно, D1К = КD = 6:2 = 3 см.
3) Через точку К проведём линию, параллельную ребру DC, и точку её пересечения с ребром С1С обозначим М1. Противоположные стороны образовавшегося прямоугольника равны между собой:
М1С = KD = 3 см (по построению)
KМ1 = DC = 6 см (по построению)
4) Треугольник МКМ1 подобен треугольнику МNC согласно признаку равенства трёх углов одного треугольника трём углам другого треугольника. А это значит, что можно составить следующую пропорцию:
ММ1 : КМ1 = МС : NC.
ММ1 = МС - М1С = 4 - 3 = 1 см
KМ1 = DC = 6 см,
МС = 4 см.
1 : 6 = 4 : NC,
откуда NC = 6 * 4 : 1 = 24 см
5) В прямоугольном треугольнике ВСN отрезок NВ является гипотенузой, а ВС = 6 см и NC = 24 см - катетами.
Следовательно, по теореме Пифагора:
NВ = √ (6^2 + 24^2) = √ (36 + 576) = √612 = 6√17, или с учетом округления, NВ ≈ 24,74 см
ответ: NВ = 6√17, или NВ ≈ 24,74 см
Получилось, что в плоскости γ через точку А к прямой b проведены две различные параллельные прямые а и с, что противоречит аксиоме. Значит предположение неверно и c пересекает β.
Объяснение:
Допустим плоскости α и β параллельны, а прямая с пересекает плоскость α в точке А.
Предположим, что эта прямая не пересекается с плоскостью β. Возьмем в плоскости β точку В и проведем плоскость γ через прямую с и точку В. Плоскость γ пересекается с плоскостями α и β по параллельным прямым а и b (теорема 17.6). Но по предположению, прямая с параллельна плоскости β, а поэтому прямая с параллельна и прямой b (теорема, обратная теореме 17.3).
Сейчас напишу
Объяснение:
1.Площадь параллелограмма =сторона *высота,сторона =15 см,значит высота= площадь/сторону=75см2/15=5см
2..Построим треугольник пусть АВС.Проведем в нем высоту ВН,получился прямоугольный треугольник(т.к высота перпендикулярна основанию и образует угол 90 градусов),в нем гипотенуза АВ=16 см,один из катетов=половине стороны АС т.к треугольник равнобедренный и высота является медианой(т.е 14/2)=7см
По теореме пифагора найдём второй катет,т.е высоту трегольника АС:
АВ^2=ВН^2+АН^2
16^2=7^2+BH^2
256=49+BH^2
256-49=207
ВН=√207≈14,39
Площадь треугольника=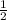 аh(половина основания на высоту)=14см/2*14,39=7*14,39=100.73см2
аh(половина основания на высоту)=14см/2*14,39=7*14,39=100.73см2
3.Построим трапецию АВСД .В трапецию можно вписать окружность,когда суммы противолежащих сторон в ней равны и трапеция равнобокая.Площадь трапеции равна S=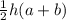
Проведём высоту.Она=2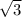 .Образовался прямоугольный треугольник.Высота(дана)также является катетом.Она лежит против угла в 30 градусов,значит по теореме она равна половине гипотенузы.Гипотенузой здесь является боковая сторона.Она равна 2*высоту=2
.Образовался прямоугольный треугольник.Высота(дана)также является катетом.Она лежит против угла в 30 градусов,значит по теореме она равна половине гипотенузы.Гипотенузой здесь является боковая сторона.Она равна 2*высоту=2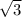 *2= 4
*2= 4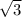 .
.
Так как трапеция равнобокая то сумма боковых сторон=4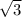 *2=16
*2=16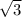 .Суммы оснований такие же.Найдем площадь:
.Суммы оснований такие же.Найдем площадь:
=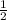 *2
*2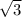 *16
*16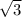 =3*16=48см2
=3*16=48см2
Остальное не вышло(