Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.
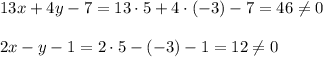
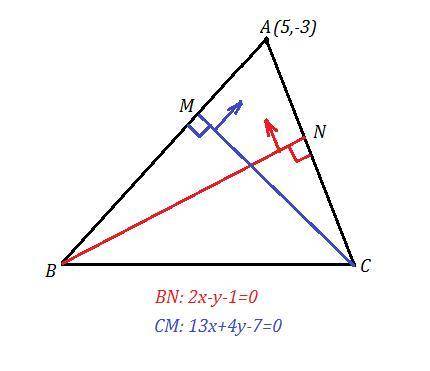
Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.
BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN:  .
.
Точка А(5,-3)∈АС и уравнение АС имеет вид:
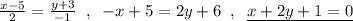
CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ:  .
.
Точка А(5,-3)∈АВ и уравнение АВ имеет вид:
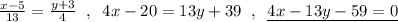
Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .
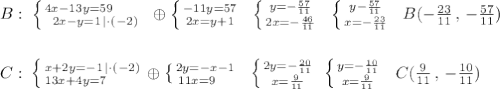
1) 3,5
2)18
Объяснение:
И в первом, и во втором случае прямая AB является касательной и радиус проведённый к касательной(OB) перпендикулярен ей т.е. образуется прямоугольный треугольник AOB.
В первом задании радиус будет равен 3,5 см т.к. ∠OAB = 30 ( теорема об угле в 30 градусов)
Во втором же задании мы просто находим гипотенузу(AB) по теореме Пифагора (AB²=8²+2√65²=64+260=324;√AB=18)