В решении этой задачи применима теорема Пифагора.
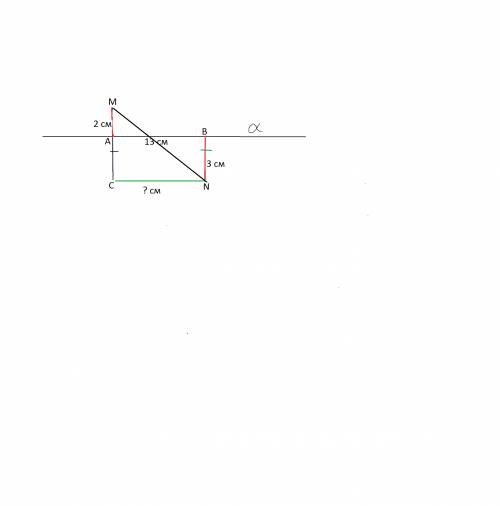
Смотрите рисунок, данный во вложении.
Если продолжить расстояние от точки А - проекции М на прямую α -
на длину расстояния от точки N до ее проекции В,
и соединить конец С этого отрезка с N,
получим прямоугольный треугольник MСN,
в котором известны гипотенуза MN=13 см,
и меньший катет МС=2+3=5 см
Если знаете несколько из Пифагоровых троек, а это как раз такая тройка (13,5,12), то, возможно, догадаетесь, что СN =12 см
По теореме Пифагора:
СN²=MN²- МС²= 169-25=144
СN=12 см
АВ=СN=12 см
ответ: Искомое расстояние равно 12 см
Находим высоту СЕ =√(13²-5²)=12
Из вершины В опустим высоту ВТ и найдем отрезок АТ нижнего основания, заключенного между высотой и боковой стороной.
√(15²-12²)=9
Тогда нижнее основание равно ДЕ+ЕТ+ТА=5+3+9=17
Площадь произведению высоты на полусумму оснований.
(3+17)*12/2=120/ед.кв./