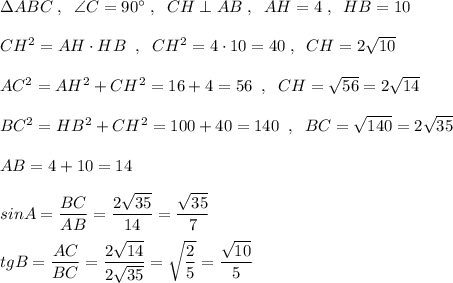
1.
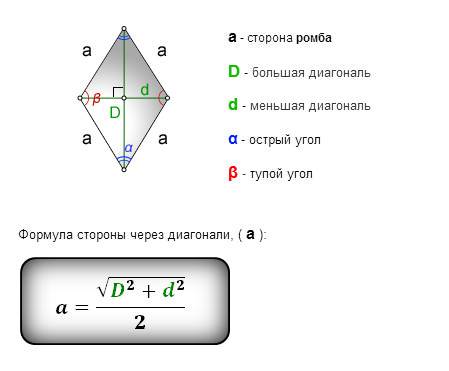
Формула в 1 вложении.
а=5, d=6
D^2 = 4a^2 - d^2
D=8
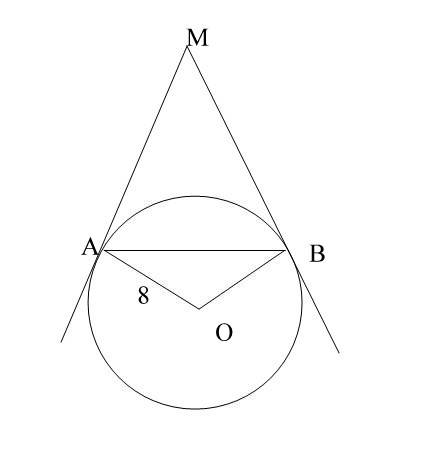
2.
Ма и Мв-касательные, АВ-секущая.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Т.е. угол МАВ=60 гр. и угол МВА=60 гр. Следовательно, треугольник АМВ-равносторонний.
Проведем из т.О перпендикуляр ОЕ к секущей АВ.
Рассмотрим треугольник АЕО-прямоугольный.
АО=r=8, угол ОЕА=90 гр, угол АОЕ=60 гр, следовательно, угол ОАЕ=30 гр.
Катет, лежащий напротив угла 30 градусов, равен половине гипотенузы.
ОЕ=1/2АО
ОЕ=4
AE^2 = AO^2 - OE^2
АЕ=корень из 48.
АВ=АЕ+ЕВ=2 корня из 48=8 корней из 3.
Р=3*8 корней из 3 = 24 корня из 3.
ответ первого пользователя верный. Но так как он очень лаконичный, даю более подробное решение.
Хорда, стягивающая дугу, на которую опирается центральный угол, является
основанием равнобедренного треугольника с боковыми сторонами - радиусами, и углом при вершине О, равным 60°.
Поэтому два других угла также равны 60°, и потому треугольник АОВ - не просто равнобедренный, а равносторонний.
Следовательно, хорда АВ равна боковым сторонам этого треугольника и равна радиусу окружности.
Радиус по условию задачи равен 7.
АВ=7.