R=4см
Sосн=16π см²
Sбок.=16π√2см²
Sпол.=16π+16π√2 см²
Объяснение:
∆SBA- равнобедренный <SBA=<SAB=45°
∆SOA- прямоугольный, равнобедренный.
<SOA=<ASO=45°.
SO=OA=R=4 см
Sосн=πR²=π*4²=16π см² площадь основания конуса.
∆SOA- прямоугольный.
SA- гипотенуза
SO и ОА - катеты.
По теореме Пифагора найдем
SA²=SO²+OA²=4²+4²=16+16=32
SA=√32=4√2 см апофема
l=SA=4√2 см
Sбок=πRl, где l- апофема.
Sбок=π*4*4√2=16π√2 см² площадь боковой поверхности конуса.
Sсеч=SO*BA/2=SO*2*OA/2=SO*OA=4*4= =16 см² площадь осевого сечения.
Sпол=Sосн+Sбок=16π+16π√2 см² площадь полной поверхности конуса.
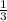BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=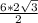
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V=9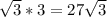
в тр-ке АВС: АВ=12, АС=21. В тр-ке АВ1С1: АС1=7, АВ1=4. У этих тр-ков угол А - общий. Остается доказать пропорциональность сторон, образующих этот угол. Отношение строим так: большая сторона к большей, меньшая к меньшей.
21/7 = 3, 12/4 = 3, Итак, стороны пропорциональны. Значит, тр-ки подобны по углу и пропорциональности сторон, образующих этот угол