mn - средняя линия
ab=cd=8
bc=6
mn = (bc+ad) / 2
уг. авс=уг. всd=120
уг. bad = уг. cda = 360-120-120=60
проведем высоту вн
рассмотри треугольник анв - прямоугольный
уг. в = 90-уг. = а=90-60=30
ан=0,5*ав=0,5*8=4 (свойство угла в 30 градусов в прямоугольном треугольнике)
проведем высоту cl
рассмотри треугольник cld - прямоугольный
уг. c = 90-уг. = d=90-60=30
dl=0,5*cd=0,5*8=4 (свойство угла в 30 градусов в прямоугольном треугольнике)
ad=ah+hl+ld
hl=bc=6
ad=4+6+4=14
mn = (6+14) / 2=20/0=10
Здравствуйте!
1).
∠1+∠2=180° смежные
∠1=2∠2 по условию
2∠2+∠2=180°
3∠2=180°
∠2=60°
∠1=2∠2=120°
2). Треугольники OBC и AOD равны по двум сторонам и углу между ними (AO=OB; CO=OD по условию; ∠СОВ=AOD -вертикальные) => ∠BCO=∠ABO как соответственные углы в равных треульниках.
AD || BC, т.к. накрест лежащие углы (∠BCO=∠ABO) равны. ЧТД.
3).
AB+AC+BC=34 см. (периметр)
AB=AC (боковые стороны)
BC (основание) =АВ+2 см= АС+ 2 см
BC+ (BC + 2 см)+(ВС+2 см) =34 см
3 ВС=30 см
ВС= 10 см
АВ=АС=10 см +2 см= 12 см
4). Треугольники АОВ и DOC равны по стороне и двум прилежащим углам (АО=ОD; ∠A=∠D по условию; ∠AOB=DOC вертикальные)
5). Проведем отрезок BD. Треугольники ABD и BDC- равнобедренные (AB=AD; BC=CD по условию) => ∠АВD=∠ADB и ∠CBD=∠CDB как углы при основании в р/б треугольнике.
∠В=∠АBD+∠CBD
∠D=∠ADB+∠CDB
А так как ∠АВD=∠ADB и ∠CBD=∠CDB, то ∠В=∠D.
6). Сумма острых углов прямогульного треугольника равна 90°.
∠A+∠B=90°
∠B=∠A-60° по условию
∠A+∠A-60°=90°
2∠A=150°
∠A=75°
∠B=∠A-60°=75°-60°=15°
7). Найдем ∠B. Сумма углов треугольника равна 180°.
∠А+∠В+∠С=180°
70°+55°+∠B=180°
∠B=180°-125°
∠B=55°
То есть ∠В=∠С=55°. А если углы в треуголнике равны, то треугольник равнобедренный. Основание BC.
7.1). Рассмотрим треугольник BMC. Он прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠С+∠МBC=90°
55°+∠MBC=90°
∠MBC=35°
∠ABC=∠ABM+∠MBC
55°=∠ABM+35°
∠ABM=20°
Объяснение:
Найдем координаты вектора АВ
АВ(х;у;z) = AB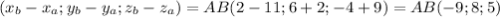
AC)x;y;z)=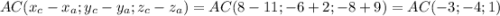
По условию перпендикулярности веторов векторы перпендикулярны, если скалярное произведение векторов равно нулю. Скалярное произведение по координатам вычислить легко, нужно перемножить соответствующие координаты и сложить их:
Раз скалярное произведение равно нулю, то АВ перпендикулярно АС