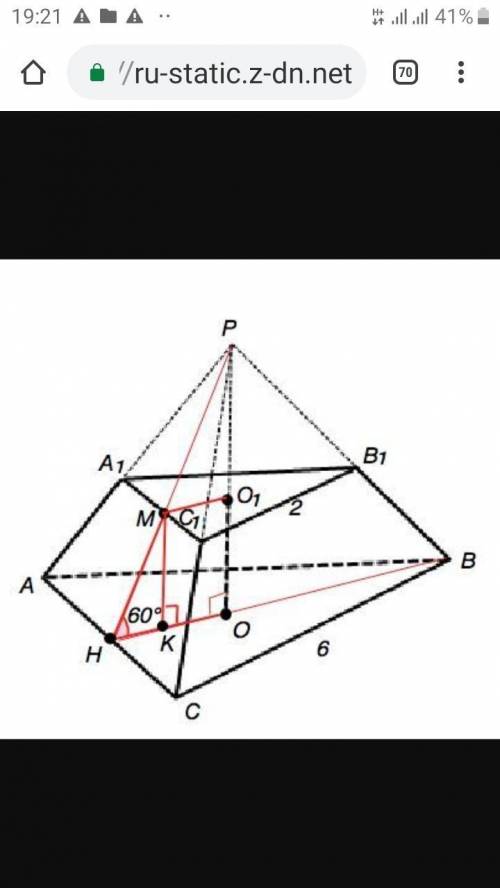
Объяснение:

Боковыми гранями правильной усеченной пирамиды являются равные равнобедренные трапеции. Для нахождения площади боковой поверхности нужно найти высоту этих трапеций.
Проведем из вершин В и В1 оснований пирамиды высоты (медианы) ВН и В1М. В треугольнике АВС т.О - центр вписанной окружности и делит ВН в отношении 2:1, считая от вершины (по свойству медиан). ОН=ВН:3=АВ•sin60°:6. ОH=6•√3:2):3.=√3
Аналогично находим длину МО1 в меньшем основании А1В1С1. Отрезок МО1=(√3)/3.
Из т.М опустим перпендикуляр МК на ОН.
НК= НО-МО1=√3-(√3)/3= (2√3)/3
МК - катет прямоугольного треугольника МКН с гипотенузой МН=НК:cos ∠МНК=[(2√3):3]:1/2=4/√3 .
По т. о 3х- перпендикулярах МН⊥АС и является высотой трапеции АА1С1С.
Площадь боковой поверхности данной пирамиды Ѕ(ус.пир.)=3•Ѕ(АА1С1С)=3•МН•(А1С1+АС):2.
Ѕ(ус.пир.)=3•(4:√3)•8:2=16√3 см²
————
Для нахождения высоты полной пирамиды РАВС, из которой получена данная усеченная пирамида, рассмотрим ∆ РОН и ∆ МНК. Они прямоугольные, имеют общий острый угол при вершине Н, ⇒
∆ РОН ~∆ МНК. k=НО:НК=√3:(2√3)/3=3/2
РО:МК=3/2.
МК=МН•sin60°=(4/√3 )•√3/2=2 см ⇒
PO=3 см
V = 6224,272 * √3 π см³
Объяснение:
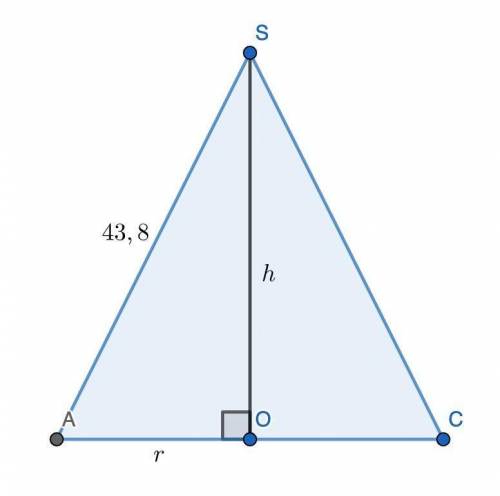
Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².
Объём конуса вычисляется по формуле 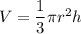 . Из предыдущего уравнения r² = 43,8² - h². Подставим это в уравнение объёма:
. Из предыдущего уравнения r² = 43,8² - h². Подставим это в уравнение объёма:
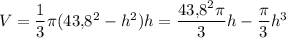
Найдём максимальное значение с производной:
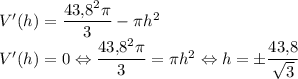
Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При 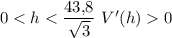 , при
, при 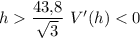 . Значит,
. Значит, 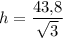 — точка максимума. При данном значении h объём конуса максимален.
— точка максимума. При данном значении h объём конуса максимален.
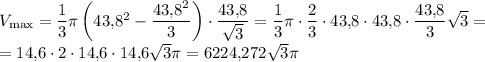
ответ:якщо а=5,b=13,sin a=√2/2,то 5*13*√2/2=65√2 ~45,96194
.
2
Объяснение: