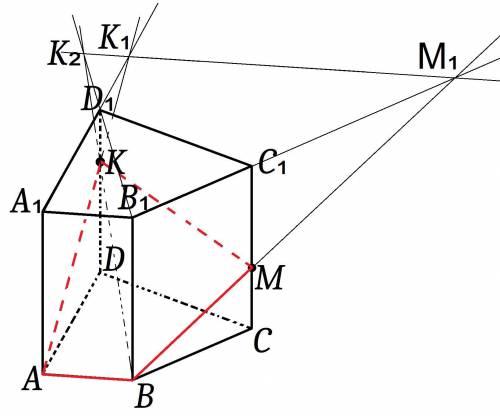
AK , A₁D₁ ⊂ (ADD₁)
Найдём пересечение этих прямых: AK ∩ A₁D₁ = K₁
BK , B₁D₁ ⊂ (BDD₁)
Найдём пересечение этих прямых: BK ∩ B₁D₁ = K₂
K₁ ∈ AK ⊂ (ABK); K₂ ∈ BK ⊂ (ABK) ⇒ K₁K₂ ⊂ (ABK).
K₁ ∈ A₁D₁ ⊂ (B₁C₁D₁); K₂ ∈ B₁D₁ ⊂ (B₁C₁D₁) ⇒ K₁K₂ ⊂ (B₁C₁D₁);
K₁K₂ , B₁C₁ ⊂ (B₁C₁D₁)
Найдём пересечение этих прямых: K₁K₂ ∩ B₁C₁ = M₁
M₁ ∈ B₁C₁ ⊂ (BCC₁); B ∈ (BCC₁) проведём прямую через две точки, лежащие в одной плоскости с ребром CC₁
Получаем, что BM₁ ∩ CC₁ = M.
M₁ ∈ K₁K₂ ⊂ (ABK); B ∈ (ABK) ⇒ BM₁ ⊂ (ABK); M ∈ M₁B ⊂ (ABK) ⇒ M ∈ (ABK).
ABMK - нужное, четырёхугольное, сечение.
CC₁ = 3,5 см.
Объяснение:
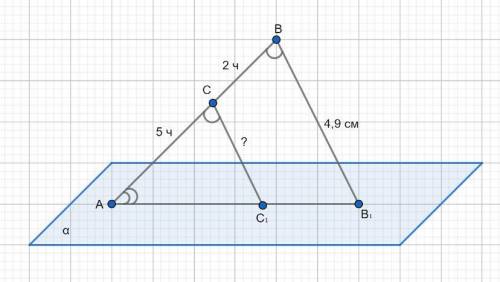
1) Теорема: через две пересекающиеся прямые проходит плоскость и притом только одна. ⇒ Прямые AB и AB₁ лежат в одной плоскости.
2) Аксиома: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
По условию точки A, B₁ и C₁ принадлежат плоскости ΔABB₁ и плоскости α. ⇒ Точки A, B₁ и C₁ лежат на одной прямой AB₁.
3) Отрезок CC₁ ║BB₁ по условию. Тогда ΔABB₁ подобен ΔACC₁ по двум углам: ∠A общий, ∠ACC₁ = ∠ABB₁ как соответствующие при CC₁ ║BB₁ и секущей AB₁ .
Из подобия треугольников следует:
AB / AC = BB₁ / CC₁;
На отрезок AB приходится 7 частей (5+2=7), на отрезок AC приходится 5 частей по условию.
7 / 5 = 4,9 см / CC₁; CC₁ = (4,9 см * 5 ) / 7 = 0,7 см * 5 = 3,5 см.
CC₁ = 3,5 см.
Прямоугольник - параллелограмм.
Если в параллелограмме диагонали перпендикулярны, этот параллелограмм - ромб. Если в ромбе все углы прямые, этот ромб - квадрат.