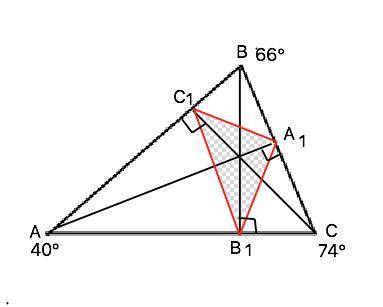
ответ: ∠С1А1В1=100°; ∠А1В1С1=48°; ∠В1С1А1=32°
Объяснение:
Треугольник, образованный основаниями высот некоторого треугольника, называется ортотреугольником. .
В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник, подобный данному (теорема).
1) ∆ С1ВА1~∆ АВС, ∠ВС1А1=∠С=74°, ∠ВА1С1=∠А=40°
2) ∆ АС1В1~∆ АВС, ∠АС1В1=∠С=74°, ∠ АВ1С1=∠ В=66°
3) ∆А1СВ1~ ∆ АВС, ∠СА1В1=∠А=40°, ∠СВ1А1=∠ В=66°
Основания высот на сторонах ∆ АВС являются вершинами развёрнутых углов
Из угла АС1В -∠В1С1А1=180°-2•74°=32°
Из ВА1С - ∠С1А1В1=180°-2•40°=100°
Из СВ1А - ∠ А1В1С1=180°-2•66°=48°
.
Пирамида правильная четырёхугольная. Значит, её основание - квадрат ABCD с диагональю AC = 6 см. Диагональ квадрата делит его углы пополам. Значит, треугольник ABC - равнобедренный (AB=BC, угол BAC = углу BCA). К тому же, треугольник ABC - прямоугольный. Тогда по т.Пифагора
Площадь основания ABCD
Диагональное сечение пирамиды - равнобедренный треугольник (две стороны - ребра пирамиды, третья - диагональ основания). Площадь этого треугольника