ответ: АС=5, АВ=ВС=15
=РЕШЕНИЕ ПРИЛОЖЕНО=

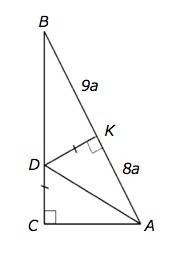
∆ АDК и АDС прямоугольные и равны по катету ( DС=DК -дано) и общей гипотенузе АD. ⇒
АК=АС и углы САD=КAD,⇒
АД - биссектриса угла ВАС.
Примем коэффициент отношения АК:КВ равным а. Тогда АВ=9а+8а=17а., АС=АК=8а
По т.Пифагора ВС=√(АВ²-АС²)=√225a²=15a
Периметр АВС=17а+15а+8а=40а
40а=80
а=2
СВ=30, АС=16, АВ=34 .
Биссектриса угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:
СД:ДВ=АС:АВ
Примем CD=х
х:(30-х)=16:34
34х=480-16х
50х=480
х=9,6 (ед. длины)
Пусть х - АС, тогда 3х - АВ и ВС.
Периметр равен 35 см.
х + 3х + 3х = 35
7х = 35
х = 5
5 см - АС.
АВ = ВС = 5 × 3 = 15 см.
ответ: 15 см, 15 см, 5 см.