Определить радиус окружности, определённой уравнением x^2+y^2-4x-6y-3=0.
ответ:Радиус окружности равен 4 условных единицы.
Объяснение:Для начала вспомним общий вид уравнения окружности:
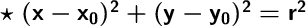
где (x₀;y₀) - координаты центра окружности, r - её радиус.
Мы имеем уравнение окружности. Чтобы найти радиус, нам нужно сделать два полных квадрата в этом уравнении по формулам квадратов разности либо суммы:
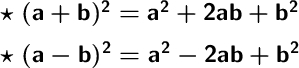
Распишем уравнение окружности по этим формулам:
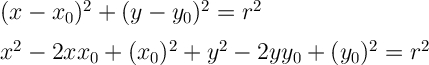
В нашей формуле окружности мы имеем x^2 и y^2, а так же 4x и (-6у). Не сложно догадаться, что (-4х) это и есть то самое (-2хх₀), а (-6у) это (-2уу₀). Отсюда находим координаты середины окружности:
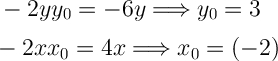
Мы нашли координаты центра нашей окружности - (-2;3).
Теперь нам нужно сделать так, чтобы в нашем уравнении окружности было всё, чтобы сделать там полные квадраты - (х+2)^2 и (y-3)^2.
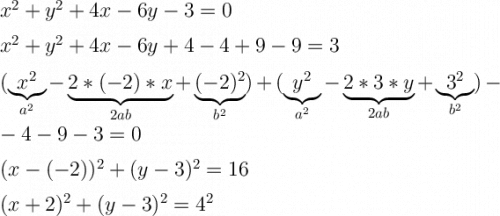
Мы преобразовали наше уравнение окружности. Его центр, как мы уже определили - (-2;3), а радиус - 4.
Объяснение:
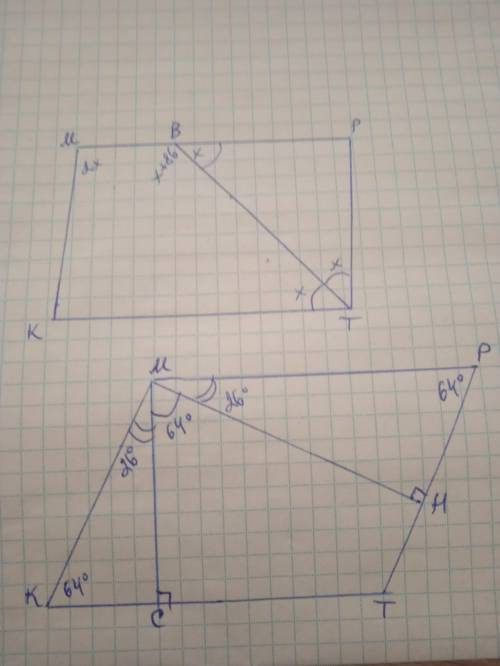
1) Дано: КМРТ - паралелограм, ТВ - бісектриса, ∠МВТ-∠ВТР=86°.
∠К, ∠М, ∠Р, ∠Т - ?
Бісектриса кута паралелограма відсікає від нього рівнобедрений трикутник, отже ΔВРТ - рівнобедрений, ∠РТВ=∠РВТ=х°;
∠РТВ=∠ВТК=х° за визначенням бісектриси
∠МВТ=х+86°
КМВТ - трапеція, сума кутів, прилеглих до бічної сторони трапеції, становить 180°, отже х+х+86=180; 2х=94; х=47.
∠М=∠Т=47*2=94°
∠Р=∠Т=180-94=86°
Відповідь: 86°, 94°, 86°, 94°
2) Дано: КМРТ - паралелограм, МС і МН - висоти, ∠К=∠Р=64°. ∠СМН - ?
ΔКСМ - прямокутний, ∠КМС=90-64=26°
ΔРМН - прямокутний, ∠РМН=90-64=26°
∠К+∠КМР=180°; ∠КМР=180-64=116°
∠СМН=116-26-26=64°
Відповідь: 64°
Объем цилиндра равен площадь основания, умнож. на высоту, площадь круга равна πд²/4, т.к. диаметр равен высоте, то
πд³/4=500, откуда высота, и она же равна диаметру может быть найдена так. Диметр равен высоте, равен д=∛(2000/π)=10∛(2/π )/см/, тогда радиус такой банки равен 5∛2/π/см/
Объяснение: