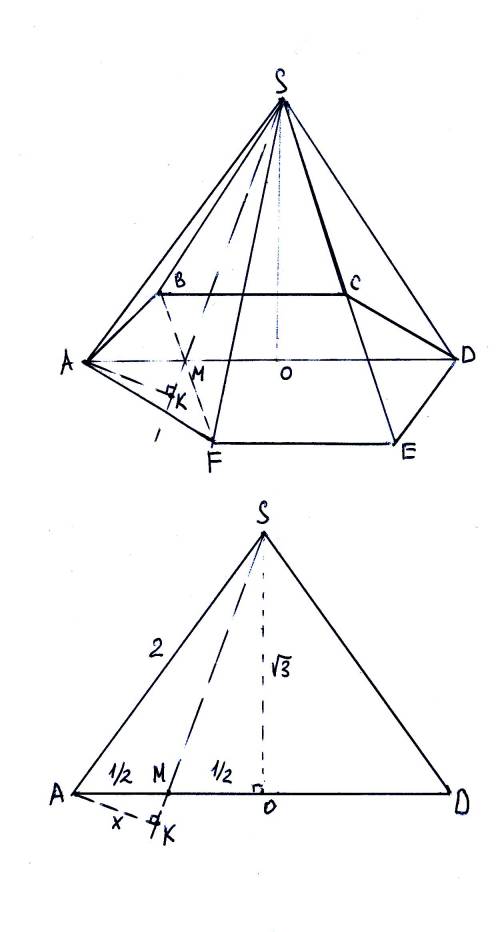
см. чертеж, верхний рисунок.
Я не буду тратить время на объяснение простых вещей - постарайтесь обосновать их самостоятельно, это очень просто.
BF перпендикулярно AD (обоснуйте), SO перпендикулярно основанию, а - значит - и BF. Поэтому => BF перпендикулярно плоскости ASD (то есть всем прямым в этой плоскости).
Если в плоскости ASD провести перпендикуляр АК к продолжению SM (М - середина BF), то АК и есть расстояние от А до SBF, поскольку АК перпендикулярно BF и SM, то есть всей плоскости SBF.
см. чертеж, нижний рисунок.
Это - плоскость ASD. В ней AD = 2 (обоснуйте), поэтому треугольник ASD - равносторонний (все стороны равны 2).
Треугольники АМК и SMO подобны (прямоугольные с равными острыми углами), поэтому АК/AM = SO/SM;
AK = x; AM = MO = 1/2;
SM^2 = 3 + (1/2)^2 = 13/4; SM = √13/2;
2*x =2*√3/√13; x = √(3/13);
Стороны квадрата "отрезают" от исходного треугольника два прямоугольных треугольника, подобных ему. Можно взять любой из них, и из пропорций, следующих из подобия, определить сторону квадрата.
Если обозначить сторону квадрата а, то стороны одного из "отрезанных" треугольеников 3 - x и x, а соответствующие стороны исходного треугольника 3 и 5, поэтому
(3 - x)/x = 3/5; 15 - 5*x = 3*x; x = 15/8; ну, а периметр квадрата 4*х = 15/2;
В общем случае, если катеты a и b, то P = 4*a*b/(a + b); это выражение симметрично относительно а и b, поэтому ответ в задаче, конечно же, не зависит от того, какой из двух "отрезанных" треугольников использовать. :)