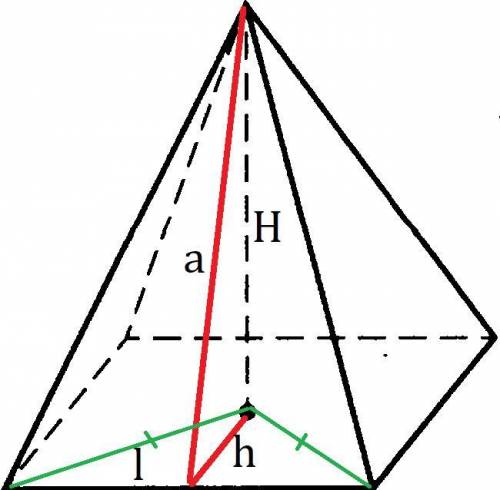
У правильной четырёхугольной пирамиды в основании лежит квадрат, а основание высота пирамиды является центром квадрата. Зная сторону квадрата (l) можно найти его диагональ - 10√2. Найдём высоту (в одном из 4 треугольников, которые образуются при пересечении диагоналей квадрата) из середины квадрата:
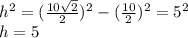
В принципе это и так логично, ведь диагональ квадрата составляет 45° с его сторонами. Теперь мы можем найти апофему пирамиды (её основание будет совпадать с основание недавно проведённой высоты т.к. это высота и медиана в равнобедренном треугольнике)
a - апофема (высота боковой грани).
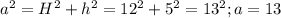
Пирамида правильная, поэтому все боковые грани равные треугольники, найдём площадь.
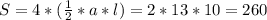
l - сторона основания.
ответ: 260 см².
r=S:p, где р - полупериметр треугольника.
Так как МN - средняя линия треугольника, сторона ВС равна 2 MN=10
Зная длину всех сторон треугольника, по теореме Герона найдем его площадь.
Площадь тругольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c):
S=√(p (p−a) (p−b) (p−c))
Не буду приводить вычисления, каждый сможет их сделать самостоятельно.
Площадь треугольника, найденная по формуле Герона, равна 36
r=S:p
r=36:((17+9+10)/2)==36:18=2