40 см и 25 см
Объяснение:
Дано:
Прямоугольный треугольник АВС (угол С - прямой):
гипотенуза АВ = 130 см
катет ВС = 104 см
Найти:
длины отрезков, на которые биссектриса меньшего острого угла делит медиану, проведенную к гипотенузе.
Решение.
1) По теореме Пифагора найдём длину катета АС:
АС = √(АВ²-ВС²) = √(130²-104²) = √(16900-10816) = √6084= 78 см
2) В треугольнике меньшая сторона лежит против меньшего угла. Это значит, что меньшим острым углом является ∠В, против которого лежит катет АС.
3) Выполним построение.
Из угла В проведём биссектрису, которая пересечет катет АС в точке Е. Из вершины прямого угла С проведём медиану к гипотенузе АВ, и точку пересечения медианы со стороной АВ обозначим D, а точку пересечения медианы CD с биссектрисой ВЕ обозначим F.
В принятых обозначениях необходимы найти DF и FC.
4) Теорема. В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Следовательно:
DC = АВ : 2 = 130 : 2 = 65 см
Так как точка D является серединой АВ, согласно построению, то:
BD = АВ : 2 = 130 : 2 = 65 см
5) Теорема. Биссектриса данного угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.
Следовательно:
DF : FC = DB : BC (1)
Так как DC = DF + FC = 65 cм, то
DF = DC - FC = 65-FC (2)
Подставим (2) в (1), получим:
(65-FC) : FC = DB : BC
(65-FC) : FC = 65 : 104
65 · 104 - 104FC = 65FC
6760 = 65FC + 104FC
169 FC = 6760
FC = 6760 : 169 = 40 см
Отсюда DF = 65-FC = 65 - 40 = 25 см
ответ: биссектриса меньшего острого угла делит медиану, проведённую к гипотенузе, на два отрезка длиной (считая от вершины прямого угла) 40 см и 25 см.
угол В
Объяснение:
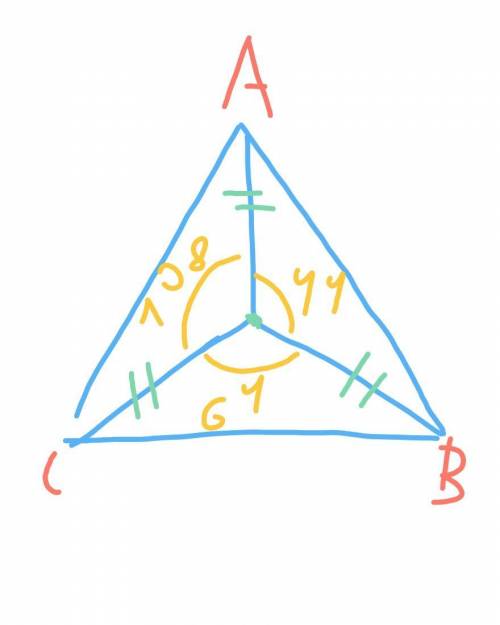
АО=ВО=СО
значит, треуг. АОВ, ВОС и СОА равнобедренные
получается:
угол ОАВ=угол ОВА=(180°-44°):2=136°:2=68°
угол ОВС=угол ОСВ=(180°-64°):2=116°:2=58°
угол ОАС=угол ОСА=(180°-108°):2=72°:2=36°
теперь, узнаем величину каждого угла:
угол А=угол ОАВ+угол ОАС=68°+36°=104°
угол В=угол ОВС+угол ОВА=58°+68°=126°
угол С=угол ОСА+угол ОСВ=36°+58°=94°
126>104>94
только тут кое-что не складывается: математически всё правильно, я перепроверила, но проблема в том, что сумма углов треугольника равна 180°. если мы сложим 104°, 126° и 94°, то получится гораздо большее число. видимо, либо так и задумано, либо это ошибка в задаче.
надо провести две высоты в трапеции и обозначить полученные маленькие отрезки как Х, т. к трапеция равнобокая
из этого составить уравнения в треугольниках (по теореме пифагора)
а площадь находится как половина произведения основание трапеции на её высоту
Объяснение: