Объяснение:
1.
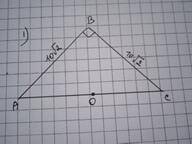
Дано: ΔАВС - прямокутний, ∠В=90°, АВ=ВС=10√2. R - ? r - ?
АС²=АВ²+ВС²=(10√2)² + (10√2)² = 200+200=400; АС=20.
Центр описаного кола припадає на середину гіпотенузи, отже
R=АО=ОС=20:2=10 од.
r=(a+b-c)/2=(10√2 + 10√2 - 20)\2 = (20√2 - 20)/2 = (20√2 - 1)/2 = 10√2 - 1 од.
2.
Катети трикутника а, в, гіпотенуза с. Тоді за умовою
а+в+с=24; а²+в²+с²=200; а²+в²=200-с², за теоремою Піфагора а²+в²=с²
200-с²=с²; 200=2с²; с²=100; с=10 см.
а+в+10=24; а+в=24-10=14 см.
Нехай а=х, тоді в=14-х.
х²+(14-х)²=10²
х²+196-28х+х²-100=0
2х²-28х+96=0
х²-14х+48=0
х=8 та х=6
а=8 см; в=6 см
S=1/2 * 8 * 6 = 24 cм²
Площадь ∆ABK S=AB*KP/2. Т.к. ∆АВС – равнобедренный, то высота ВМ является биссектрисой.
КР=КН=3. Из ∆АPК по Пифагору AP²=AK²-KP²=25-9=16 => AP=4.
В ∆АВН ВK - биссектриса и делит сторону АН на отрезки, пропорциональные сторонам АВ и ВН:
AK/AB=KH/BH. AB=BP+AP=BH+4 (BP=BH) => 5/(BH+4)=3/BH, 5*BH=3*BH+12 => BH=6 и AB=6+4=10.
Тогда S=10*3/2=15.