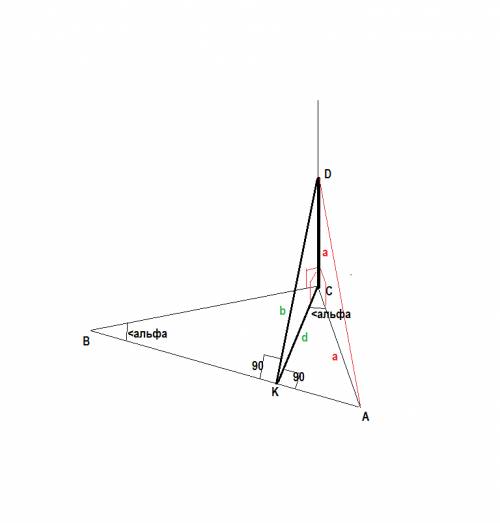
сделаем построение по условию
перпендикуляр к плоскости - это отрезок DC=a
<C=90 ; катет АС =а ; <B = <(альфа)
гипотенуза AB
DK ┴ AB
CK ┴ AB
DC ┴ CK
по теореме о трех перпендикулярах СK - это проекция DC
DK=b, CK=d -расстояние от концов отрезка DC до гипотенузы
так как прямые (СК)┴(АВ) ;(BС)┴(АC) взаимно перпендикулярные,то <KCA=<B=<альфа
∆KAC - прямоугольный
d = a*cos<альфа
∆KDC - прямоугольный
по теореме Пифагора
b = √ (d^2+a^2) =√((a*cos<альфа)^2+a^2) = a*√((cos<альфа)^2+1)
ответ
d = a*cos<альфа
b = a*√((cos<альфа)^2+1)
Объяснение:
1) Рассмотрим треугольники EFD и CFD:
EF=CF, <EFD= <CFD - по условию, DF - общая.
Следовательно треугольники равны по двум сторонам и углу между ними ( І признак равенства треугольников).
Из равенства треугольников следует равенство сторон и углов: DE=DC, <EDK=<CDK.
2) Рассмотрим треугольники EDK и CDK:
DE=DC, <EDK=<CDK - доказано в п.1, DK - общая.
Треугольник EDK = треугольнику CDK по двум сторонам и углу между ними ( І признак равенства треугольников).
Из равенства треугольников следует равенство углов: <DEK=<DCK, что и требовалось доказать.