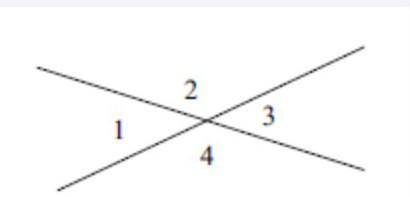
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.
Объяснение:
Разместим внутри нашего квадрата маленькие квадратики, как показано на рисунке. Попробуем найти количество таких квадратиков и длину стороны каждого, чтобы общая сумма их периметров была равна 1992.

Обозначим число маленьких квадратиков вдоль стороны через N, а длину сторон маленьких квадратиков через A. Сумма периметров этих квадратиков будет равна 4N2A, а нам надо, чтобы эта сумма была равна 2020, т.е. 4N2A = 2020. Поскольку вдоль большого квадрата размещается N квадратиков со стороной A, то NA  1 и NA < 1. Значит, 4N > 1992 и 4N  2020 т.е. N  498. Взяв N = 500, A = 0, 002020, получим набор квадратиков, сумма периметров которых будет равна 0, 0020204500500 = 2020, что и требовалось.
Угол С поделён пополам биссектрисой, поэтому его половину принимаем за х, тогда угол А, равный углу С (треугольник -то равнобедренный!) будет 2х. Сумма углов тр-ка ADC 180 град. (как и у любого тр-ка). Составим ур-ие: X+2X+60=180
3х=120
х=40
угол А=80 град,угол С=80 град, угол АВС=180-2х80=20 град
ответ: 80град,80 град,20 град