Радиусы оснований усеченного конуса равны 2 и 6 см, образующая наклонена к плоскости основания под углом 45. Найдите объем и площадь полной поверхности.
2. Дано: <EAC=<DCA DF=EF Доказать, что ΔABC-равнобедренный. Док-во: 1. Так как <EAC=<DCA (по условию), то ΔAFC- равнобедренный. Отсюда AF=FC. Так как DC=DF+FC и AE=AF+EF, то DC=AE. 2. ΔDCA=ΔEAC (по 1-ому признаку равенства Δ: DC=EA, <EAC=<DCA (по условию); AC-общая сторона). Из равенства Δ следует, что <DAC=<ECA. <DAC=<BAC <ECA=<BCA. Отсюда <BAC=<BCA. Значит ΔABC-равнобедренный. Что и требовалось доказать.
2. Дано: <EAC=<DCA DF=EF Доказать, что ΔABC-равнобедренный. Док-во: 1. Так как <EAC=<DCA (по условию), то ΔAFC- равнобедренный. Отсюда AF=FC. Так как DC=DF+FC и AE=AF+EF, то DC=AE. 2. ΔDCA=ΔEAC (по 1-ому признаку равенства Δ: DC=EA, <EAC=<DCA (по условию); AC-общая сторона). Из равенства Δ следует, что <DAC=<ECA. <DAC=<BAC <ECA=<BCA. Отсюда <BAC=<BCA. Значит ΔABC-равнобедренный. Что и требовалось доказать.
Объяснение:
Дано: DO1 (R) =6 см, AO (r)=2 см, ∠ADA1=45°
Решение
Проведем высоту ОО1. Тогда AOO1D — прямоугольная трапеция. Проведем AA1⊥DO1. АОО1А1 — прямоугольник, так что AO=A1O1=r.
Тогда DA1=DO1-A1O1=R-r.
Далее, в прямоугольном треугольнике ΔDAA1 ∠ADA1=45°, так что ∠DAA1=90°-∠ADA1=45°. Поэтому ΔDAA1 — равнобедренный и прямоугольном треугольник.
Тогда DA1=AA1=H конуса=R-r=6-2=4
V=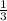 *π *H (
*π *H (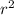 + (r*R)+
+ (r*R)+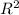 )=
)=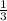 *4*π(
*4*π(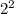 +(2*6)+
+(2*6)+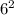 )=
)= 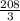 *π см3
*π см3
Чтоб найти S пов. сначала найдем твірну (L)
L=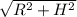 =
=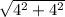 =4
=4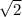 см
см
S пов.= π(r+R)*L+π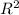 +π
+π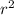 =8π(
=8π(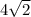 +5)
+5)