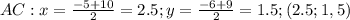

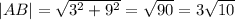
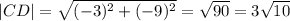
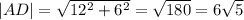
Первый .
Для решения применим теорему косинусов для треугольника.
ВС2 = АВ2 + АС2 – 2 * АВ * ВС * CosA.
ВС2 = 9 + 36 – 2 * 3 * 6 * (1 / 2).
ВС2 = 45 – 18 = 27.
ВС = √27 = 3 * √3 см.
Второй .
Проведем высоту ВН.
В прямоугольном треугольнике АВН катет АН лежит против угла 300, тогда АН = АВ / 2 = 3 / 2 = 1,5 см. СН = АС – АН = 6 – 1,5 = 4,5 см.
Тогда ВН2 = АВ2 – АН2 = 9 – 2,25 = 6,75.
В прямоугольном треугольнике ВСН, ВС2 = ВН2 + СН2 = 6,75 + 20,25 = 27.
ВС = √27 = 3 * √3 см.
ответ: Длина стороны ВС равна ВС 3 * √3 см.
Объяснение:
Правильная четырёхугольная пирамида.
∠SHO = 60˚
SO = 2√3
Найти:S полн. поверхности - ?
Решение:SH - апофема.
"Апофема - высота боковой грани правильной пирамиды, проведённая из вершины пирамиды".
△SHO - прямоугольный, так как SO - высота.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катера на √3".
=> SO = OH * √3 = 2√3 => OH = 2
"Сумма острых углов прямоугольного треугольника равна 90°".
=> ∠OSH = 90˚ - 60˚ = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> SH = OH * 2 = 2 * 2 = 4
Так как данная пирамида - правильная, четырёхугольная => основание данной пирамиды - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> АВ = ВС = AD = DC
AB = BC = AD = DC = 2 * OH = 2 * 2 = 4
S квадрата = 4² = 16 ед.кв.
Р - периметр квадрата.
Р = a * 4 = 4 * 4 = 16
S бок поверхности = 1/2Р * h = 16/2 * 2√3 = 16√3 ед.кв.
S осн = S квадрата.
S полн поверхности = S бок поверхности + S осн = 16√3 + 16 = 16(√3 + 1) ед.кв.
ответ: 16(√3 + 1) ед.кв.