
Докажите, что сумма любых двух соседних углов (углов, которые "прилегают" к одной стороне) параллелограмма равна 180°.
- - -
Параллелограмм - это четырёхугольник, у которого противоположные стороны (стороны, не имеющие общих вершин) параллельны.
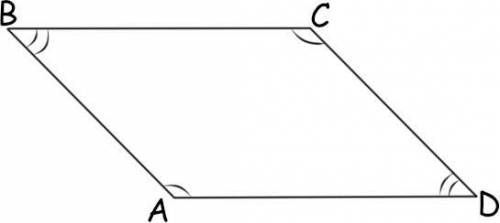
На рисунке -
AB║CD, BC║AD.
Сначала рассмотрим прямые AB и CD когда они пересечены секущей СВ. Так как AB║CD (по условию), то внутренние односторонние ∡В и ∡С в сумме дают 180° (свойство односторонних углов при параллельных прямых).Теперь рассмотрим эти же прямые когда они пересечены секущей AD. Аналогично, внутренние односторонние углы ∡A и ∡D в сумме дают 180°.Теперь сделаем так.
Так как -
∡B+ ∡C = 180°
∡A + ∡D = 180°
Но также по свойству параллелограмма мы знаем, что противоположные углы параллелограмма равны (на рисунке отмечены дугами), то из выше написанного соотношения мы получаем, что -
∡A + ∡B = 180°
∡C + ∡D = 180°.
- - -
Что требовалось доказать!
Правильный треугольник имеет поворотную симметрию 3-го порядка (на 120°). Центр этой симметрии совпадает с центром описанной окружности, так как вершины треугольника при повороте остаются лежать на окружности. Фигура, полученная пересечением правильного треугольника и его повернутой на 60° копии, имеет поворотную симметрию 6-го порядка, так как при повороте её на 60° начальный треугольник перейдёт в повёрнутый, а тот перейдёт в начальный.
Сторона треугольника образует со своей повёрнутой копией угол 60°, следовательно, треугольники отрезают друг от друга шесть одинаковых из-за симметрии правильных треугольников со стороной 1/3 - три стороны треугольников образуют сторону исходного треугольника.
Тогда полученная фигура - правильный шестиугольник (из-за поворотной симметрии 6-го порядка и углов по 120°) со стороной 1/3.