Пусть М - любая точка плоскости. Пусть каждое из расстояний от точки М до вершин выпуклого четырехугольника меньше 2, тогда АМ+ВМ+СМ+DМ<2+2+2+2=8 (*)- сумма расстояний от точки М до вершин выпуклого четырехугольника,
по неравенству треугольника имеем AM+BM>AB AM+DM>AD BM+CM<BC CM+DM>CD сложив получим что 2(AM+BM+CM+DM)>AB+BC+CD+AD откуда учитывая (*) получаем AB+BC+CD+AD<8
аналогично AB+AD>BD BC+CD>BD AB+BC>AC AD+CD>AC или сложив 2(AB+BC+CD+AD)>2*(BD+AC) AC+BC+CD+AD>BD+AC получается что 8>AC+BC+CD+AD>BD+AC=8 противоречие/ Откуда получаем что уловие задачи истинно
Точка Е - середина основания ВС, точка К - середина оскования АД. Значит на отрезке ЕК лежит точка М. Для начала рассмотрим две трапеции, на которые отрезок ЕК поделил трапецию АВСД. Трапеции АВЕК и КЕСД равновеликие, поскольку у них равны верхние и нижние основания и высота (так как Е и К середины оснований). Известно, что медиана делит треугольник на два равновеликие треугольника. ОК - медиана треуг. АМД, ОЕ - медиана треуг. ВМС. Треуг. АМК и ДМК равновеликие. Треуг. ВМЕ и СМЕ также равновеликие. Получается, что если от трапеций АВЕК и КЕСД отнять равновеликие треуг. АМК, ВМЕ и ДМК, СМЕ, то в результате останутся два равновеликие треуг. АМВ и СМД. Доказано.
√77см
Объяснение:
Т.к. BD - высота, то треугольник ABD - прямоугольный. Тогда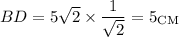
. Аналогично треугольник BDC прямоугольный. По теореме Пифагора 
.
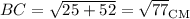Задача решена!