Точка пересечения серединных перпендикуляров треугольника является центром окружности, описанной около этого треугольника. Так как данный треугольник — равнобедренный, то по теореме о медиане равнобедренного треугольника медиана, биссектриса и высота треугольника, проведенные к основанию, совпадают. Значит, высота совпадает с серединным перпендикуляром, проведенным к основанию треугольника. Следовательно, центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.
Объяснение:
Теорема о 30-градусном угле такова: Катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть катет BC — равен половине гипотенузы AB.
Но нам эта информация не в решении задачи, продолжим.
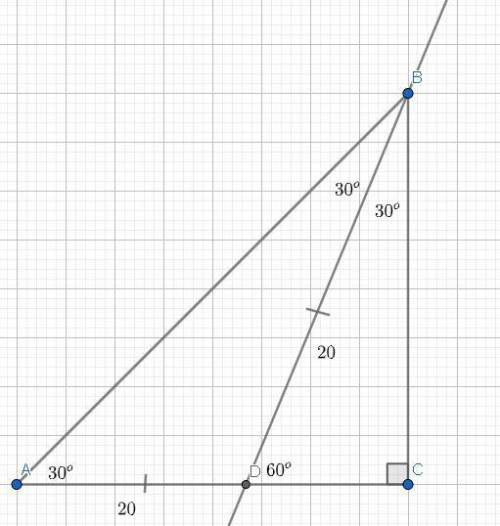
<B = <C - <A = 90-30 = 60°.
BD биссектриса — делит угол B — пополам, тоесть: <ABC == <DBC = 60/2 = 30°.
<A == <ABD = 30° => AD == DB; треугольник ABD — равнобедренный.
BD = 20 => AD == BD = 20.
<BDC = 30° => DC = DB/2 (теорема о 30-градусном угле прямоугольного треугольника).
DB = 20 => DC = 20/2 = 10
AD = 20; DC = 10 => AC = 10+20 = 30.
Вывод: AC = 30.
Объяснение: если треугольник прямоугольный то вычислим его большую сторону. ВС и АВ вычеслены на фото. Вычислим величину АС по такой же формуле: АС²=(-1-3)²+(0-(-4)²=(-4)²+4²=
=16+16=32; АС=√32=4√2. Итак большая сторона - это ВС, которая является в этом треугольнике гипотенузой и лежит напротив прямого угла, которым является угол А. ∆АВС с прямым углом А, угол В и С- острые. Косинус - это отношение прилежащего к углу катета к гипотенузе.
Решение на фото