Question

Дана ломаная ABCG такая, что BC=5AB, CG=4AB, ∠ABC=∠BCG=90∘. Точки D, E , F разбивают отрезок CG на четыре равные части. Найдите сумму углов, под которыми виден отрезок AB из точек C, D, E, F, G.

Answer 1

45°

Объяснение:

∠ABC =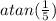 $atan(\frac{1}{5})$

∠ABD =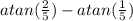 $atan(\frac{2}{5}) - atan(\frac{1}{5})$

Аналогично остальные углы.

Складываем:

$atan(\frac{1}{5}) + atan(\frac{2}{5}) - atan(\frac{1}{5}) +atan(\frac{3}{5}) - atan(\frac{2}{5}) + atan(\frac{4}{5}) - atan(\frac{3}{5}) + atan(\frac{5}{5}) - atan(\frac{4}{5}) = atan(\frac{5}{5}) = 45 deg$

============      

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"    

Бодрого настроения и добра!      

Успехов в учебе!