1. Да. Сумма двух всегда должна быть больше третьей.
б)Да
в) нет. 8+9 меньше 45
ответ а. 5; 5; 5. Да или Нет
б. 5; 8; 9. Да или Нет
в. 8; 9; 45. Да или Нет
2. х+х+2х=180, х=180/4=45, углы D и Е равны по 45, а Р 90 градусов.
ответ
∡ D = 45°;
∡ E = 45°;
∡ P = 90°.
3 Если основание х, то две боковые стороны по (х+30) , а периметр это сумма всех сторон, тогда х+х+30+х+30=330, 3х=270, х=90. значит, основание 90см, а боковые стороны по 30+90=120/см/
ответ AB= 90 см;
CB= 120см;
AC= 120см.
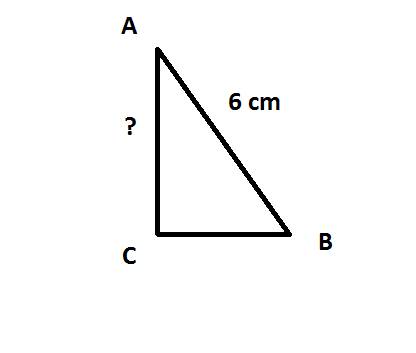
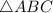 . Из условия ясно, что он — прямоугольный (так как
. Из условия ясно, что он — прямоугольный (так как 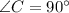 ).
). 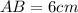 — гипотенуза,
— гипотенуза, 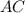 — искомый катет,
— искомый катет, 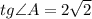
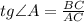
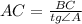
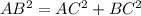
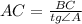 .
.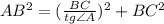
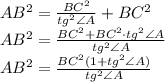
 :
: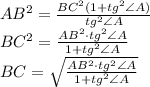
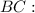
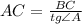
 новую подстановку:
новую подстановку: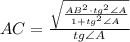
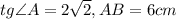
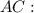
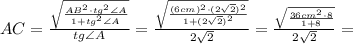
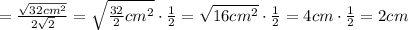

Во первых, хорда не должна превышать размера диаметра окружности. Сначала нужно с циркуля измерить длину отрезка, потом совместить с диаметром окружности, не изменяя раствора циркуля. В случае, если второй конец циркуля выходит за пределы окружности, задача не имеет решения.
Во-вторых, если вышеуказанное не выполнилось, то надо совместить первую ножку циркуля, не меняя раствор циркуля, с любой точкой на окружности, а второй ножкой циркуля подобрать другую точку на окружности. Вообще-то, если отрезок меньше диаметра окружности, то получатся две искомые точки, или два отрезка. В случае же, когда отрезок равен диаметру точки В и С совпадают.
Вот и все.
Объяснение:
1. Задание
Сумма двух сторон треугольника должна быть больше третьей стороны.
а) 5+5=10; 10>5, да такой треугольник существует называется правильный треугольник.
б)5+8=13; 13>9
5+9=14; 14>8
8+9=17; 17>5
Да такой треугольник существует.
в)
8+9=17; 17<45 нет такой треугольник не существует.
2. Задание
1+1+2=4 коэффициент.
Сумма углов в треугольнике равна 180°
180°:4=45
45*1=45° градусная мера одного угла
45*1=45° градусная мера второго угла
45*2=90° градусная мера третьего угла.
Или решение уравнением.
Пусть градусная мера одного угла будет <1=х, тогда градусная мера второго угла будет <2=х, а градусная мера третьего угла <3=2х. Составляем уравнение
х+х+2х=180°
4х=180°
х=180°:4
х=45° градусная мера первого и второго угла.
Градусная мера третьего угла равна 2х, подставляем значение х.
2*45°=90°
ответ: градусная мера углов в треугольнике равна <D=45°;<E=45°;<P=90°
3. Задание.
Треугольник равнобедренный.
Пусть основание треугольника будет х, тогда боковая сторона будет х+30(так как треугольник равнобедренный то таких сторон две.) Составляем уравнение
х+2(х+30)=330
х+2х+60=330
3х=330-60
3х=270
х=270:3
х=90 см. Основание треугольника (АВ).
Боковая сторона (СВ=АС) равно
х+30, подставляем значение х.
90+30=120 см. боковая сторона треугольника.
ответ : АВ=90см; СВ=120см; АС=120см.
Проверка
90+120+120=330 (периметр треугольника)