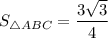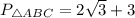
; 
Объяснение:
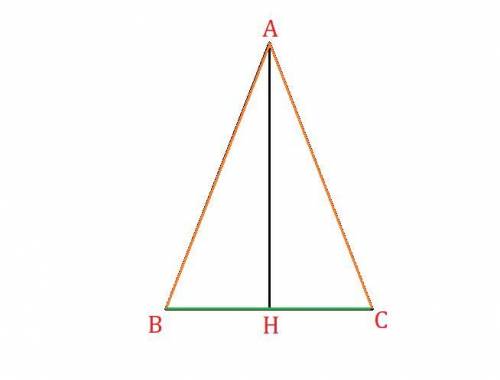
Обозначим данный равнобедренный треугольник буквами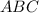 
.
==========================================================
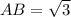
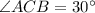
Проведём высоту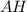 
к основанию 
.
============================================================
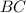Так как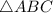 
- равнобедренны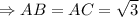й 
и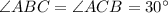 
, по свойству.
===========================================================
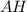- высота, медиана, биссектриса 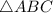, по свойству.
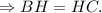
Рассмотрим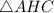 
:
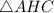- прямоугольный, так как 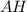- высота.
Если угол прямоугольного треугольника равен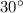 
, то напротив лежащий катет равен половине гипотенузы.
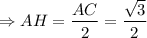
Найдём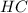 
, по теореме Пифагора:
==========================================================
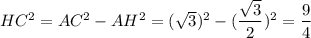
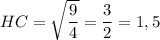
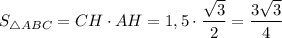
Так как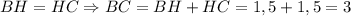 
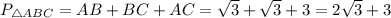
1. Площадь треугольника равна половине произведения стороны на высоту, проведенную к ней. S=0.×12×3×12=36×6=216
2. По т. Пифагора: второй катет=5
Площадь прямоугольного треугольника равна половине произведения первого катета на второй катет. S=0.5×5×12=30
По т. Пифагора: сторона ромба в квадрате: 25+36=61
Сторона ромба=√61
Периметр:4√61
Площадь равна половине произведения диагоналей на синус угла между ними, в ромбе угол - прямой, его синус 1. S=0.5×10×12=60
Отметьте как лучший ответ, если не сложно ❤️