
180°.
Объяснение :
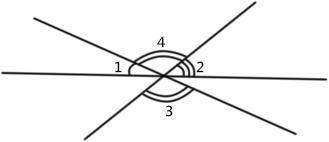
В сумме ∠1, ∠2, ∠4 дают градусную меру развёрнутого угла, то есть 180°.
Также ∠4 и ∠3 - вертикальные (по определению). Помним, что вертикальные углы равны, то есть ∠3 = ∠4.
Обобщим выше сказанное -
∠1 + ∠2 + ∠4 = 180°, но так как ∠3 = ∠4 ⇒ ∠1 + ∠2 + ∠3 = 180°.
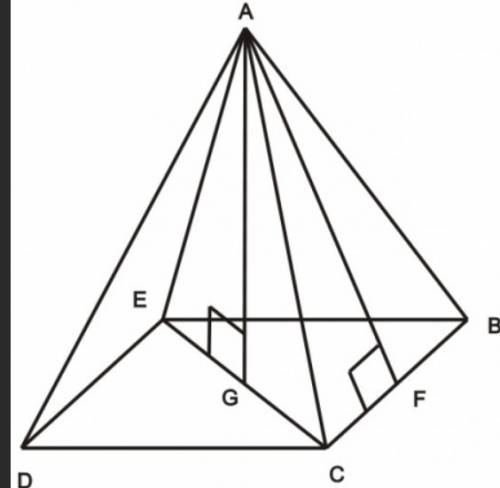
Боковое ребро, высота и половина диагонали основания образуют прямоугольный треугольник GСА,, угол GСА в нем 30*, а напротив угла в 30* находится катет равный половине гипотенузы.
АG=AC/2
AG=6/2
AG=3
Для нахождения объёма нужно знать не только высоту, но и площадь основания, по теореме Пифагора найдём её, так как второй катет равен ее половине, умножим результат на 2.
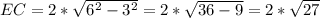
Основание правильной четырёхугольной пирамиды — квадрат, найдём его площадь через диагонали,которые между собой равны.
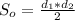
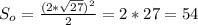
Теперь можем найти объём:
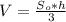
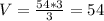
Пусть имеем прямоугольную трапецию АВСД и вписанную окружность с центром в точке О и радиусом r.
Центр вписанной окружности находится на пересечении биссектрис острого и тупого углов трапеции.
Треугольник СОД - прямоугольный (по свойству трапеции).
Сторона СД = √(15² + 20²) = 25 см.
Высота h треугольника СОД равна радиусу r.
r = h = 15*20/25 = 12 см (по свойству площади).
Сумма оснований равна сумме боковых сторон.
Средняя линия равна: Lср = (2*12 + 25)/2 = (49/2) см.
Площадь трапеции равна: S = hLср = 24*(49/2) = 588 см².
180, потому что угол 3 равен углу, лежащему между 1 и 2(как вертикальные), а угол 1 плюс угол угол 2 плюс угол между 1 и 2 равен 180(по рисунку)