Через точку, расположенную внутри треугольника, проведены прямые, параллельные сторонам треугольника. Эти прямые разбивают треугольник на три
треугольника и три четырёхугольника. Параллельные высоты трёх получившихся
треугольников равны 5, 6, 7. Найдите параллельную им Высоту исходного
треугольника.

👇

Увидеть ответ

Ответ:

лев652

10.04.2023

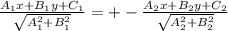
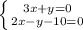
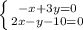
Из параллелограммов видно, что

a1 +a2 +a3 =A

Стороны параллельны - все треугольники подобны исходному.

a1/A =h1/H, ...

a1/A +a2/A +a3/A =A/A => h1/H +h2/H +h3/H =H/H => h1 +h2 +h3 =H

То есть H =5+6+7 =18

Через точку, расположенную внутри треугольника, проведены прямые, параллельные сторонам треугольника

4,7(97 оценок)

Открыть все ответы

Ответ:

sashenkakoster

10.04.2023

По уравнениям боковых сторон 3x+y=0 и -x+3y=0 видно, что они проходят через начало координат - это одна из вершин треугольника: О(0;0).
Основание равнобедренного треугольника перпендикулярно его высоте (она же и биссектриса угла при вершине).
Находим уравнения биссектрис угла при вершине О:
$\frac{A_1x+B_1y+C_1}{ \sqrt{A_1^2+B_1^2} } =+- \frac{A_2x+B_2y+C_2}{ \sqrt{A_2^2+B_2^2} }$
1) (3х+у)/√10 = (-х+3у)/√10
3х+у = -х+3у
4х = 2у
у = 2х не подходит (проходит выше сторон треугольника).

2) (3х+у)/√10 = -(-х+3у)/√10
3х+у = -(-х+3у)
2х = -4у
у = (-1/2)х.
Уравнение перпендикулярной прямой у = 1/(-к)+в
В нашем случае уравнение основания (назовём его АВ) будет таким:
у = 1(1/2)х+в = 2х+в.
Подставим координаты известной точки на основании (5;0):
0 = 2*5+в отсюда в = -10.
Уравнение АВ: у = 2х-10 или 2х-у-10 = 0.
Координаты вершин А и В находим как как точки пересечения боковых сторон с основанием.
$\left \{ {3x+y=0} \atop {2x-y-10=0}} \right.$
Сложив уравнения, получаем 5х-10 = 0, отсюда х = 10/5 = 2.
у = -3х = -3*2 = -6. Это точка А(2; -6).
$\left \{ {{-x+3y=0} \atop {2x-y-10=0}} \right.$
Умножим первое уравнение на 2 и сложим:
5у = 10, у = 10/5 = 2, х = 3у = 3*2 = 6.
Это точка В(6; 2).

ответ: вершины треугольника О(0;0), А(2;-6), В(6;2).

4,4(28 оценок)

Ответ:

зубрильчик

10.04.2023

Пусть P - точка пересечения AM и CD; и пусть BP пересекает AC в точке Q;
тогда из теоремы Чевы сразу следует
AQ/QC = AD/DB = 3;
из теоремы Ван-Обеля (следствие теоремы Чевы)
AP/PM = AD/DB + AQ/QC = 6;
Получилось, что в треугольнике CAM 1) угол С = 60°; 2) высота CP делит сторону AM на отрезки в отношении 6:1; 3) AC = 3; этого достаточно, чтобы решить задачу.
Если для краткости записи обозначить CP = h; MP = z; MC = y; AC = a = 3; то легко записать очевидные соотношения
y^2 = z^2 + h^2;
a^2 = (6*z)^2 + h^2;
(7*z)^2 = y^2 + a^2 - a*y; (это просто теорема косинусов, косинус 60° равен 1/2; напоминаю, что a = 3)
вычитая из второго уравнения первое, легко найти
a^2 - y^2 = 35*z^2;
остается исключить z, подставить a = 3; и получится квадратное уравнение для y; напомню, что ВС = 2*y;
(y^2 + a^2 - a*y)/49 = (a^2 - y^2)/35;
5*y^2 + 5*a^2 - 5*a*y = 7*a^2 - 7*y^2;
12*y^2 - 2*a^2 - 5*a*y = 0;
12y^2 - 15*y - 18 = 0; или BC^2 - (5/2)*BC - 6 = 0;
BC = 5/4 + √((5/4)^2 + 6) = (5 + √(25 + 16*6))/4 = (5 + 11)/4 = 4; (второй корень отпадает)

4,6(45 оценок)

Это интересно:

Кулинария-и-гостеприимство

21.02.2023

Секреты приготовления вкусного соуса для макарон...

Образование-и-коммуникации

01.01.2022

Как найти площадь прямоугольника: простое объяснение и формула...

Кулинария-и-гостеприимство

14.02.2022

Как приготовить кислое молоко: правила и рекомендации...

Компьютеры-и-электроника