ответ: 11
Объяснение:
Так как ABCD параллелограмм, то BC || AD ⇒ ордината точки C совпадает с ординатой точки B (равной 8)
Пусть абсцисса точки C равна x, тогда C имеет координаты (x; 8)
По формуле расстояния между точками составим уравнение для A и C:
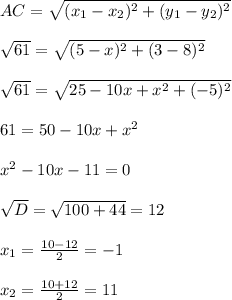
Так как ABCD параллелограмм, то BC = AD = 3 ⇒ абсцисса точки B меньше на 3, чем абсцисса точки C. Чтобы ∠ BAD был острым, нужно, чтобы абсцисса точки B была больше абсциссы точки А.
На основе найденных x, найдём абсциссы точки B:
При x = -1: -1 - 3 = -4 < 5 -- угол тупой (не подходит)
При x = 11: 11 - 3 = 8 > 5 -- угол острый
1)-12x²-(-3x⁶+8-10x²)=-12x²+3x⁶-8+10x²=-2х²+3x⁶-8
2) 9m³-5m+(m-6m³-2m⁴)= 9m³-5m+m-6m³-2m⁴=3m³-4m-2m⁴
3) 5x(x+4)-x•(6-2x²) =5x²+20x-6x+2x³=5x²+14x+2x³=
4) -y²•(2y-6)+4y•(y²-y) =-2y³+6y²+4y³-4y²=2y³+2y²
1) (4-x)(4+x)(16+x²)=(16-x²) *(16+x²)=256-x⁴
2) (a²-5b)(a²+5b)(5y-x) =(a⁴-25b²)*(5y-x)=5a⁴y+a⁴x-125b²y+25b²x
3)3x• (12x-4y)-(6x-y)² =36x²-12xy-36x²+12xy-y²=-y²
4)(2x-5y)²+4x•(5y-x)=4x²-20xy+25y²+20xy-4x²=25y²