<Х=118°
Объяснение:
∆ABD- прямоугольный треугольник, т.к. <АВD вписанный угол опирается на дугуАD=180°
Сумма острых углов в прямоугольном треугольнике равна 90°
<DAB+<BDA=90°
<DAB=90°-<BDA=90°-28°=62°
<DAB- вписанный угол опирается на дугуВD(меньшая)
Тогда дугаВD(меньшая)=2*<DAB=2*62°=124°
Вся окружность составляет полный угол который равен 360°
дугаВD(меньшая)+дугаВD(боль)=360°
ДугаВD(боль)=360°-дугаВD(меньшая)=
=360°-124°=236°
<ВСD- вписанный угол опирается на дугуВD(боль)
<ВCD=дугаВD(боль):2=236°:2=118°
Обозначение:
дугаВD(боль)- большая дугаBD
Объяснение:
1) Так как искомый центр гомотетии лежит на одной прямой с точками Х и X', то для нахождения центра проведем прямую XX'.
Условия заданий приводятся в учебных целях и в необходимом объеме — как иллюстративный материал. Имя автора и название цитируемого издания указаны на титульном листе данной книги. (Ст. 19 п. 2 Закона РФ об авторском праве и смежных правах от 9 июня 1993 г.)
2) Так как N = 2, то по определению гомотетии ОХ' = 20Х, где О — центр гомотетии, значит, отложим от точки X' отрезок ОХ' = 2ОХ и получим искомую точку О.
ответ:4см
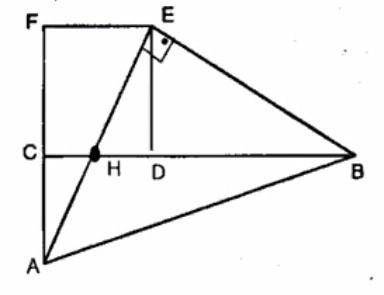
Решение: Из условия: СF=CD=FE=ED=2м(как стороны квадрата)
так как CH=HD, то НD=1/2СD=1м.
Так как ED- высота в прямоугольном треугольнике к гипотенузе ,
то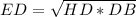
или ED²=HD*DB → DB=ED²:HD= 2²:1=4(см)
(само доказательсво чему равна высота в прямоугольном треугольнике к гипотенузе есть много вариантов по поиску: "Формула длины высоты через составные отрезки гипотенузы")