ответ
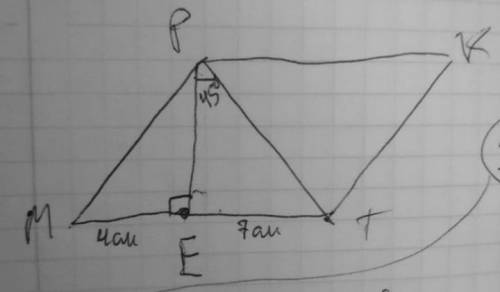
3. В параллелограмме MPKT на стороне MT отмечена точка E, =∠PEM=900, ∠EPT=450, МЕ = 4 см, ЕТ = 7 см. Найдите площадь параллелограмма
4,0/5
9
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
PE перпендикулярна к MT, PE — высота.
S = MT * PE
MT = ME + ET = 4см + 7см = 11см
Рассмотрим треугольник PET. ∠PET = 90°, ∠EPT = 45°. По свойству углов в треугольнике, ∠PTE = 180° – ∠PET – ∠EPT = 180° – 90° – 45° = 45°.
∠PTE = ∠EPT = 45°, получается треугольник PET — равнобедренный, значит PE = ET = 7см.
S = MT * PE = 11см * 7см = 77см^2
думаю правильно если нет извини
Вот........
ЭТА ЗАДАЧА ПО ГЕОМЕТРИИ КАК ДОКАЗАТЬ
ТУТ ПИШЕМ ПРЯМО ЧТО МЫ ДЕЛАЕМ А ПОТОМ И РЕШАЕМ.
Если не понятен почерк вот решение
Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они прямоугольные, углы HAK и KAN равны, поскольку АК — биссектриса, сторона AK — общая, следовательно, треугольники равны. Тогда KN=KH=4. Аналогично, равны треугольники BKH и BKM, откуда MK=KH=4.
Найдём площадь параллелограмма как произведение основания на высоту.
S=AD*MN=AD*(MK+KN)=7*(4+4)=7*8=56
ЧТД
ответ:56см

---
Площадь поверхности пирамиды состоит из площади основания и 2-х пар равных граней - прямоугольных треугольников (⊿ MDA=⊿ MDC;⊿ MAB=⊿ MCB): АМ и МС перпендикулярны сторонам квадрата ( по т. о 3-х перпендикулярах), а МD перпендикулярна его плоскости по условию.
S полн= S АВСD+ 2S (MAВ)+2S (MCD)
2S (MAD)=(a²:2)•2=a²
2S (MАВ)=АВ•MA
MA=a√2 (треугольник МАD равнобедренный прямоугольный)
2S (MАВ)=2•(а•а√2):2=а²√2
S(ABCD)=a²
S полн=a²+а²+a²√2=a²(2+√2)
—————————————————————————
2.
Основание прямого параллелепипеда АВСDA’B’C’D' - параллелограмм АВСД, стороны которого равны а√2 и 2а , острый угол равен 45°.
Высота параллелепипеда равна меньшей высоте параллелограмма.
Найдите:
а) меньшую высоту параллелограмма;
б)угол между плоскостью АВС1 и плоскостью основания;
в)Площадь боковой поверхности параллелепипеда;
г)Площадь поверхности параллелепипеда.
а)
меньшая высота CН параллелограмма ABCD идет из вершины C к большей его стороне АВ.
∆ ВСН - прямоугольный, угол СВН=45° по условию.=>
СН=ВС•sin45°=a√2•√2/2=a
б)
Параллелепипед прямой,⇒ ребро СС’ перпендикулярно плоскости основания и сторонам и является высотой параллелепипеда.
СС’=CH=a
СН перпендикулярна АВ, С'Н⊥АВ по т. о 3-х перпендикулярах
а так как СС’=СH (по условию), треугольник НСС’ равнобедренный прямоугольный.
Угол СНС’ между плоскостью АВС1 и плоскостью основания из равнобедренного прямоугольного треугольника СНС’=45°
в)
Площадь боковой поверхности параллелепипеда равна произведению его периметра на высоту:
S бок=2•( 2а+а√2)•а=4а²+2а²√2=2а²(2+√2)
г)
Площадь поверхности параллелепипеда - сумма площадей 2-х оснований и боковой поверхности.
S (ABCD)=СH•AВ=a•2a=2a²
Оснований два.
S полн=2•2a²+2а²(2+√2)=2а²(4+√2)