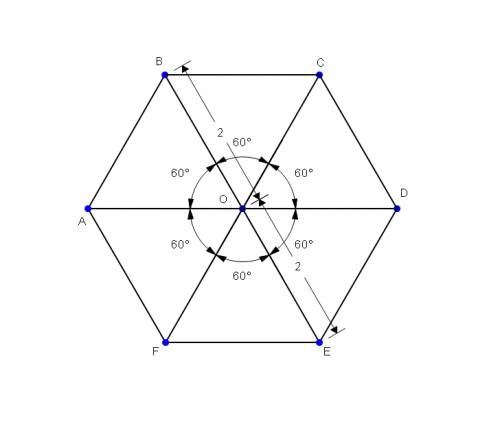
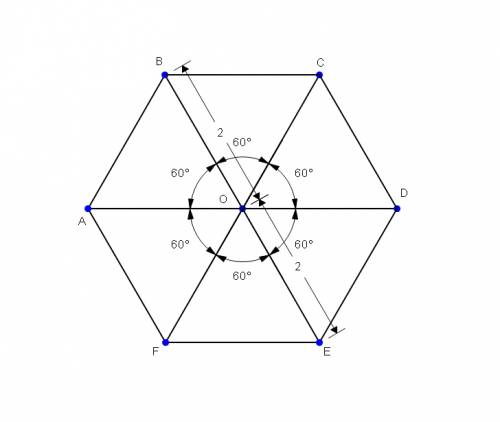
Обозначения во вложении.
Проведем в шестиугольнике все большие диагонали.
Т.к. шестиугольник правильный, то:
все его стороны равны, т.е. AB=BC=CD=DE=EF=FA
Большие диагонали пересекаются в одной точке О (центр описанной окружности)
Большие диагонали равны между собой(AD=BE=CF) и в точке О делятся пополам (AO=BO=CO=DO=EO=FO).
Исходя из этого, треугольники AOB, BOC,COD,DOE,EOF,FOA равны между собой по трем сторонам и являются равносторонними. Угол AOB=360/6=60 градусов. Площадь правильного треугольника равна S=a^2*(корень квадратный из 3)/2
а=2, S=корень квадратный из 3
Площадь шестиугольника=6*S=6*(корень квадратный из 3)
3√3/2 см.
Объяснение:
Если тригонометрические соотношения в прямоугольном треугольнике ещё не изучены, можно воспользоваться этим
1. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, тогда длина гипотенузы с = 2R = 2•3 = 6(см).
2. По условию один из острых углов треугольника равен 60°, тогда второй острый угол равен 90° - 60° = 30°. Напротив него лежит катет, равный половине гипотенузы, а = 6:2= 3 (см).
3. По теореме длина второго катета b = √(36 - 9) = √27 = 3√3(см).
4. S = 1/2ab,
S = 1/2• c • h, тогда
1/2•a•b = 1/2• c • h,
ab = ch,
h = (ab)/c = (3•3√3)/6 = 3√3/2 (см).