2) 6 см 3) 38 см 4) 2 см, 4см
Объяснение:
2) Проведём из вершина другого тупого угла высоту NP. Она также отсечёт от основы MF отрезок MP=HF=2см. Значит PH=MH-MP=8-2=6см. Поскольку, проведя 2 высоты мы образовали прямоугольник PNKH, то у него NK=PH=6см
3) Т.к. AC является биссектрисой, значит <BAC=<DAC. В то же время, <DAC=<BCA как накрест лежащие при параллельных отрезках BC и AD и секущей AC. И тогда <BAC=<BCA. А значит △ABC - равнобедренный и AB=BC.
P=AB+CD+BC+AD=8+8+8+14=38см
4) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Значит параллельные прямые a и c отсекли и на стороне AE равные отрезки AD=DE. Значит AD=2см, AE=AD+DE=2+2=4см.
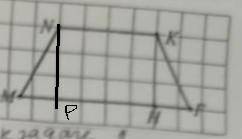
Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта.. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур.
Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.
Прямоугольный треугольник занимал почетное место в Вавилонской геометрии. Стороны прямоугольного треугольника: гипотенуза и катеты.
Термин «гипотенуза» происходит от греческого слова «ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая». Слово берет начало от образа древнегреческих арф, на которых струны натягиваются на концах двух взаимно-перпендикулярных подставок. Термин «катет» происходит от греческого слова «катетос», которое означает начало «отвес», «перпендикуляр».
Евклид говорил: «Катеты – это стороны, заключающие прямой угол».
В Древней Греции уже был известен построения прямоугольного треугольника на местности. Для этого использовали веревку, на которой были завязаны 13 узелков, на одинаковом расстоянии друг от друга. Давайте и мы попробуем построить прямоугольный треугольник.