∠A = ∠C = 55° и ∠B = ∠D = 125°.
Объяснение:
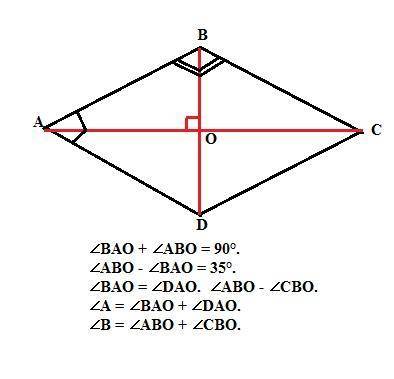
Диагонали ромба взаимно перпендикулярны. Следовательно, они со стороной ромба образуют прямоугольный треугольник. Сумма острых углов прямоугольного треугольника равна 90°, а их разность равна 35° (дано).
Пусть один из углов равен х градусов. Тогда второй равен х+35 градусов.
Значит 2х = 90-35 = 55°. И один из углов треугольника равен 55:2 = 27,5°.
Тогда второй угол равен 27,5+35 = 62,5°.
В ромба диагонали являются биссектрисами его углов. Следовательно, углы ромба равны удвоенным градусным мерам найденных углов прямоугольного треугольника.
Противоположные углы ромба равны.
Углы ромба равны 125° и 55°.
Проверка: углы ромба, прилежащие к одной стороне, в сумме равны 180°.
125+55 = 180°.
Нехай маємо прямокутний трикутник ABC (∠C=90), у якого AC=√5 см – катет і BH=4 см – проекція катета BC на гіпотенузу AB (за умовою).
прямокутний трикутник, рисунок Проведемо висоту CH=h до гіпотенузи AB (AB⊥CH).
За властивістю прямокутного трикутника
h^2= AH•BH
(це виводиться із подібності прямокутних трикутників ABC і CBH).
Нехай AH=x - проекція катета AC на гіпотенузу AB, тоді h^2=4x.
У прямокутному ΔACH (∠AHC=90), у якого AH=x і CH=h=2√x – катети, AC=√5 см – гіпотенуза, за теоремою Піфагора запишемо:
AH^2+CH^2=AC^2, x^2+4x=5, x^2+4x-5=0,
за теоремою Вієта, отримаємо
x1=1 і x2=-5<0, звідси AH=1 см.
AB=AH+BH=1+4=5 см – гіпотенуза ΔABC.
Відповідь: 5.