S ≈ 6.87 cм²
Объяснение:
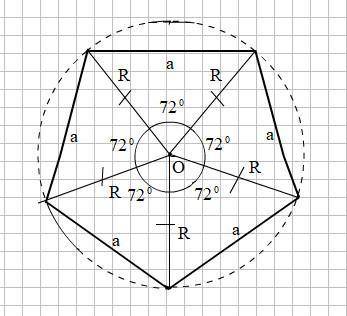
Правильный пятиугольник со стороной а = 2см состоит из пяти равных треугольников. Треугольники эти равнобедренные с боковой стороной, равной R (радиусу описанной окружности), и с углом α при вершине,
α = 180°: 5 = 72°
Углы при основании такого треугольника равны:
0.5 · 180°· (n - 2)/n = 0,5 · 180° · 3 : 5 = 54°.
По теореме синусов можно найти боковую сторону
R : sin 54° = а : sin 72°
R = а · sin 54° : sin 72° = 2 · 0.809 : 0.951 ≈ 1.7
Площадь пятиугольника
S = 5 · 0.5R² · sin 72° = 2.5 · 1.7² · 0.951 ≈ 6.87(cм²)
122° больший из углов, образованный при пересечении биссектрисы острого угла прямоугольного треугольника и противоположного катета
Объяснение:
сумма углов треугольника равна 180 градусов
Угол, который делит биссектриса равен: 180-90-26=64°
биссектриса в треугольнике делит угол пополам
64°/2 = 32° один из острых углов в треугольнике, образованном биссектрисой
180-90-32=58° меньший из углов, образованный при пересечении биссектрисы острого угла прямоугольного треугольника и противоположного катета
180-58=122° больший из углов, образованный при пересечении биссектрисы острого угла прямоугольного треугольника и противоположного катета