45°
Объяснение:
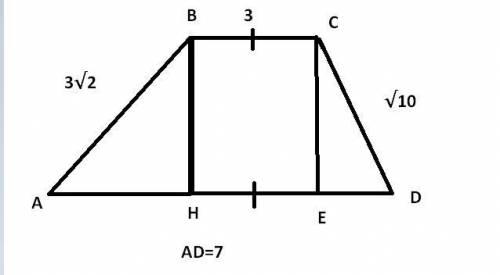
Проведём высоты BH и CE, они равны, т.к. ABCD - трапеция
AH+ED=AD-BC=7-3=4 см
3√2=√9*2=√18>√10, следует, что AB>CD и AH>ED
Возьмём AH=y, тогда ED=4-y т.к. 4-y+y=4
AH²+BH²=(3√2)²;
ED²+CE²=ED²+BH²=(√10)²
Имеем
AH²=(3√2)² - BH²
ED²=(√10)² - BH²
Подставив y, получаем
y²=18 - BH²
10 - BH²=(4-y)²=16-8y+y²
10-(16-8y+y²)=BH²=18 - y²
10-16+8y-y²=18-y²
10-16+8y=18
8y=18+16-10=24
y=24/8=3
Значит, AH=3; ED=4-3=1
BH=√AB²-AH²=√18-9=√9=3
Т.к BH - высота, то ∠AHB=90°; AH=BH=3 см⇒ΔABH равнобедренный и ∠A=∠B=90/2=45°
Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.