20°
Объяснение:
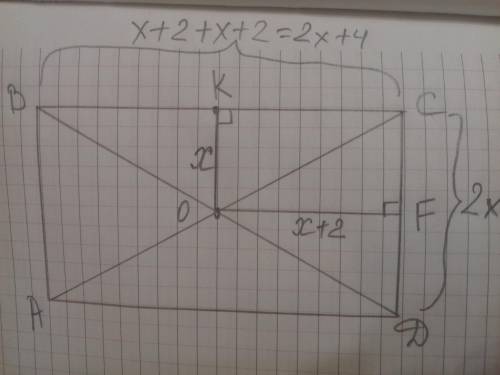
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
5
Объяснение:
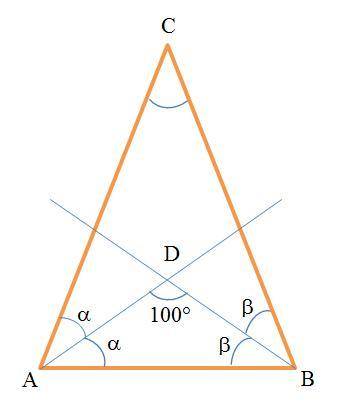
Чертёж в прикрепленном файле
Диагонали прямоугольника равны и точкой пересечения делятся пополам, образуя равнобедренные треугольники. Расстояние от точки О до сторон прямоугольника является высотами в равнобедренных треугольниках, а значит и медианами. Образовавшийся четырехугольник OKCF - прямоугольник, КО=СF= х; КС=OF= х+2,
тогда DA=ВС= ВК+КС = х+2+х+2=2х+4; AB=CD=СF+FD= х + х=2х
Периметр прямоугольника Р=АВ+ВС+СD+DA= 2х+2х+4+2х+2х+4=8х+8
По условию Р=28
8х+8=28
8х=20 разделим обе части на 4
2х=5
т.к. меньшие стороны AB=CD=2х, значит меньшая сторона равна 5.