Перша сторона АС=16см
Друга сторона АВ=20см
Третя сторона ВС=24см
Объяснение:
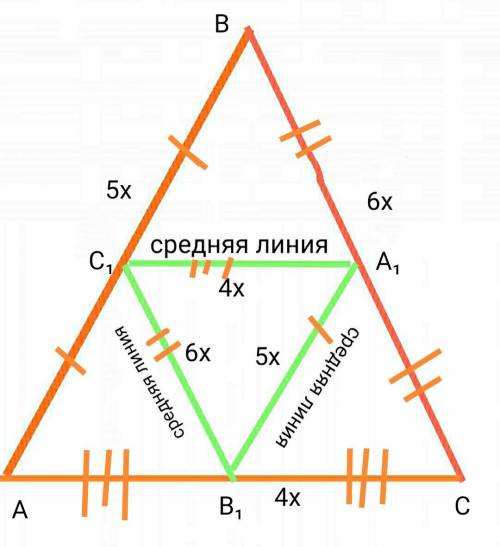
Позначемо вершини трикутника АВС, а вершини трикутника створеного середніми лініями А₁В₁С₁. Вершини ∆А₁В₁С₁ лежать на серединах сторін ∆АВС, тому вони ділять сторони ∆АВС навпіл. А також середня лінія трикутника паралельна протилежній стороні і дорівнює її половині, тому: АС₁=ВС₁=А₁В₁; АВ₁=СВ₁=А₁С₁; ВА₁=А₁С=В₁С₁, тому ∆А₁В₁С₁~∆АВС. Якщо середні лінії ∆А₁В₁С₁ відносяться як 4 : 5 : 6, то сторони ∆АВС будуть мати таке ж саме відношення. Позначемо ці відношення як 4х, 5х та 6х, і якщо відомо, що периметр трикутника 60см, складемо рівняння:
4х+5х+6х=60
15х=60
х=60÷15
х=4
Тоді перша сторона АС=4×4=16см
Друга сторона АВ=5×4=20см
Третя сторона ВС=6×4=24см
1) Окружности касаются внутренним образом, расстояние между центрами равно R-r. Окружность вписана в угол, ее центр лежит на биссектрисе, угол между линией центров и стороной равен a.
(R-r)/r= 1/sina <=> R/r= 1/sina +1 <=> r/R= sina/(sina+1)
Sк/Sс= пr^2 : пR^2*2a/360 = (r/R)^2 *180/a = (sina/(sina+1))^2 *180/a
2) AB=2R*cosa, BC=2R*sina
S=AB*BC/2 =R^2*2sina*cosa =R^2*sin(2a)
Или
Центральный угол вдвое больше вписанного, опирающегося на ту же дугу, ∠BOC=2∠BAC=2a.
S(BOC)= R^2*sin(2a)/2
Медиана делит треугольник пополам.
S(ABC)=2S(BOC) =R^2sin(2a)