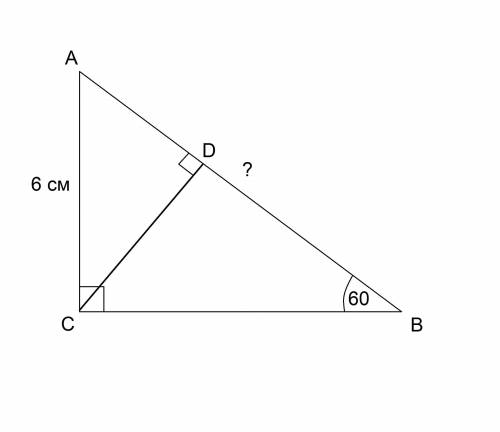
Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.
Найти: а) AB; б) CD
Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° =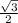 
= 
= 
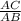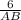; Отсюда AB = 
= 
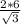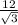см.
2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.
ответ: а)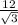 
см; б) CD = 3 см.
Находим внутренний угол В треугольника АВС:
<B=180-78=102°
Это наибольший угол треугольника (на углы А и С приходится всего 180-102=78°). Против большего угла лежит большая сторона треугольника. Значит, искомые углы ВОА и ВОС.
Поскольку ВО - биссектриса, то угол ОВA равен:
<OBA= 102:2=51°
Зная внешний угол при вершине А, находим внутренний угол треугольника:
<A=180-150=30°
Зная, что сумма углов треугольника равна 180°, находим угол ВОА в треугольнике АВО:
<BOA=180-<OBA-<A=180-51-30=99°
<BOC=<AOC-<BOA=180-99=81°