R=4см
Sосн=16π см²
Sбок.=16π√2см²
Sпол.=16π+16π√2 см²
Объяснение:
∆SBA- равнобедренный <SBA=<SAB=45°
∆SOA- прямоугольный, равнобедренный.
<SOA=<ASO=45°.
SO=OA=R=4 см
Sосн=πR²=π*4²=16π см² площадь основания конуса.
∆SOA- прямоугольный.
SA- гипотенуза
SO и ОА - катеты.
По теореме Пифагора найдем
SA²=SO²+OA²=4²+4²=16+16=32
SA=√32=4√2 см апофема
l=SA=4√2 см
Sбок=πRl, где l- апофема.
Sбок=π*4*4√2=16π√2 см² площадь боковой поверхности конуса.
Sсеч=SO*BA/2=SO*2*OA/2=SO*OA=4*4= =16 см² площадь осевого сечения.
Sпол=Sосн+Sбок=16π+16π√2 см² площадь полной поверхности конуса.
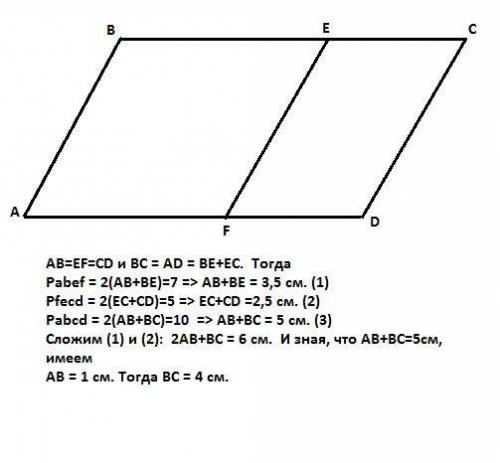
Стороны параллелограмма: АВ = CD =1см; ВС = AD = 4см.
Объяснение:
В параллелограмме противоположные стороны равны.
Пусть параллелограмм разделен на два параллелограмма отрезком EF, параллельным сторонам АВ и CD параллелограмма ABCD - параллелограммы ABEF и FECD.
АВ=EF=CD и BC = AD = BE+EC. Тогда
Pabef = 2(AB+BE)=7 => AB+BE = 3,5 см. (1)
Pfecd = 2(EC+CD)=5 => EC+CD =2,5 см. (2)
Pabcd = 2(AB+ВС)=10 => AB+ВС = 5 см. (3)
Сложим (1) и (2): 2АВ+ВС = 6 см. И зная, что АВ+ВС=5см, имеем
АВ = 1 см. Тогда ВС = 4 см.
Всё видно на скриншоте
Объяснение: