В равнобедренном треугольнике две боковые стороны равны.
Если заданы две стороны равнобедренного треугольника 12 и 6, и нет пояснения, какая из сторон боковая, а какая сторона - основание, то возможны 2 варианта .
Если неизвестная сторона -боковая, то она может быть равна 6 . Тогда в треугольнике стороны равны 6, 6, 12 .
Но для таких длин сторон треугольника не выполняется неравенство треугольника: сумма двух сторон треугольника больше длины третьей стороны; 6+6=12, но (6+6) не больше 12. Не существует треугольника со сторонами 6, 6, 12.
Если неизвестная сторона -боковая, то она может быть равна 12 . Тогда в треугольнике стороны равны 12, 12, 6 .
Неравенство треугольника выполняется: 12+12>6 , 12+6>12.
Аналогично, если неизвестная сторона - основание, то оно может быть равна или 6, или 12. Тогда две боковые стороны равны в первом случае по 12, а во втором случае по 6 . То есть опять получаем два треугольника, один со сторонами 6, 12, 12 , а второй со сторонами 12, 6, 6 , который не существует .
ответ: сторона равнобедренного треугольника может быть равна 12 .
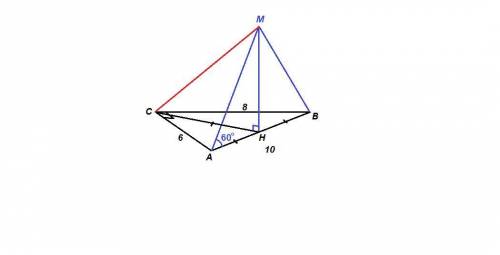
ответ: 10
Объяснение:
Так как средние линии прямоугольного треугольника АВС, параллельные катетам, равны 3 и 4, то катеты равны 6 и 8.
Гипотенуза по теореме Пифагора:
АВ = √(AC² + CB²) = √(36 + 64) = √100 = 10
Пусть Н - середина АВ. AH = HB = 5.
Тогда МН - медиана и высота равнобедренного треугольника АВМ. Так как плоскости перпендикулярны, а МН - перпендикуляр к линии их пересечения, то МН⊥(АВС), и значит МН⊥СН.
СН - медиана прямоугольного треугольника, проведенная к гипотенузе, значит, равна ее половине:
СН = 1/2 АВ = 5.
МН⊥(АВС), тогда АН - проекция МА на (АВС), значит
∠МАН = 60° - угол наклона АМ к плоскости (АВС).
ΔAMH: ∠AHM = 90°,
MH = AH · tg60° = 5√3
Из прямоугольного треугольника СНМ по теореме Пифагора:
CM = √(CH² + MH²) = √(25 + 75) = √100 = 10