Один з кутів утворений при перетині двох прямих, дорівнює 46. Знайти решту кутив

👇

Увидеть ответ

Ответ:

18alinochka150

14.08.2021

ответ: 46* и 134*.

Объяснение:

Условие:

"Один из углов образован при пересечении двух прямых, равен 46. Найти остальные углы."

При пересечении прямых образуются два типа углов: смежные и накрест лежащие.

Накрест лежащие равны между собой и равны 46*.

Сумма смежных углов равна 180*. Значит, если один из них равен 46*, то другой равен: 180*-46*=134*.

Как-то так... :)) Удачи!

4,6(76 оценок)

Открыть все ответы

Ответ:

BelkaNext

14.08.2021

Ты же понимаешь, что без чертежа объяснять несколько проблематично? Ну так вот... Наслаждайся!
1) Представь треугольник АВС с прямым углом С. Пусть угол между высотой и ближайшем к ней катетом будет x. Тогда угол между биссектрисой и этим катетом будет 15 + x. Тогда 15 +x +15 +x = 90 ==> х = 30. Рассматривая прямоугольный треугольник, образованный высотой и гипотенузой, можно заметить, что второй его угол будет равен 90 - x = 60. Это один из углов начального треугольника, значит второй угол будет равен 30 (согласен на словах все слишком каряво, так что стоит все это нарисовать)
ответ: 30; 60
2) угол 120 градусов может быть только углом, против которого лежит основание. Следовательно, углы при основании равны по 30 градусов. В полученном прямоугольном треугольнике основание - гипотенуза, а высота - катет, лежащий против угла в 30 градусов ==> высота = 4/2 = 2
ответ: 2

4,8(52 оценок)

Ответ:

LiliyaEgor

14.08.2021

Задача 1.

<PBH=15° (дано).

<CBP = 45° (BP - биссектриса прямого угла).

<CBH = <CBP+<PBH = 45°+15° = 60°. => <C = 30°(по сумме острых углов прямоугольного треугольника НВС).

<A=60°(по сумме острых углов прямоугольного треугольника AВС).

ответ: 60°, 30° и 90°.

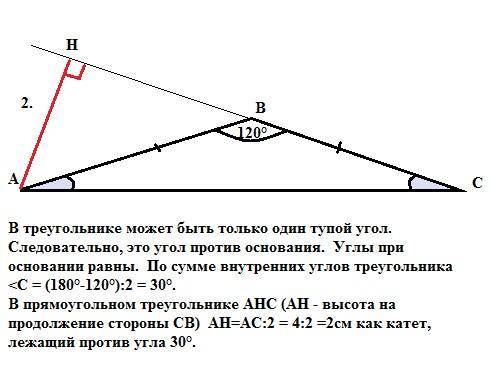
Задача 2.

В треугольнике может быть только один тупой угол. Следовательно, это угол против основания. Углы при основании равны. По сумме внутренних углов треугольника <C = (180°-120°):2 = 30°.

В прямоугольном треугольнике АНС (АН - высота на продолжение стороны СВ) АН = АС:2 = 4:2 =2см как катет, лежащий против угла 30°.

ответ: АН = 2см.

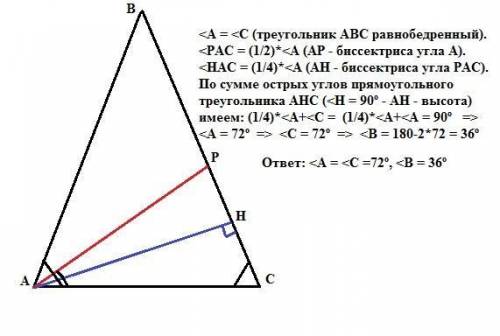
Задача 3.

<A = <C (треугольник АВС равнобедренный).

<PAC = (1/2)*<А (АР - биссектриса угла А).

<НАС = (1/4)*<A (AH - биссектриса угла РАС).

По сумме острых углов прямоугольного треугольника АНС (<Н = 90º - АН - высота) имеем: (1/4)*<A+<C = (1/4)*<A+<A = 90º =>

<A = 72º => <C = 72º => <B = 180-2*72 = 36º.

ответ: <A = <C= 72º , <B =36º .