АВ - диаметр, делит окружность пополам, и градусная мера дуги АВ равна 360º:2=180º⇒
∠АСВ=180º:2=90º, т.к. по свойству вписанного угла он равен половине градусной меры дуги, на которую опирается. ( Вписанный угол, опирающийся на диаметр, всегда прямой.) ⇒
∆ АСВ - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90º.
∠СВА=90º-70º=20º
-------
∠C=90°
∠B=20°
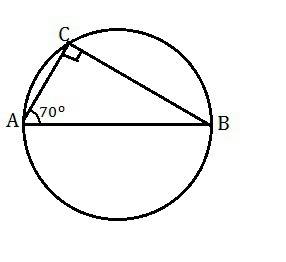
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
МР = АВ/2, ⇒
МР = АК = КВ
КР = ВС/2, ⇒
КР = ВМ = МС
КМ = АС/2, ⇒
КМ = АР = РС.
Таким образом ΔАКР = ΔКВМ = ΔРМС = ΔМРК по трем сторонам.
Для ΔАКР и ΔАВС:
∠А - общий,
∠АКР = ∠АВС как соответственные при пересечении параллельных прямых КР и ВС секущей АВ, значит
ΔАКР подобен ΔАВС по двум углам.
Значит треугольнику АВС будут подобны и все остальные треугольники, равные треугольнику АКР:
ΔКВМ подобен ΔАВС
ΔРМС подобен ΔАВС
ΔМРК подобен ΔАВС
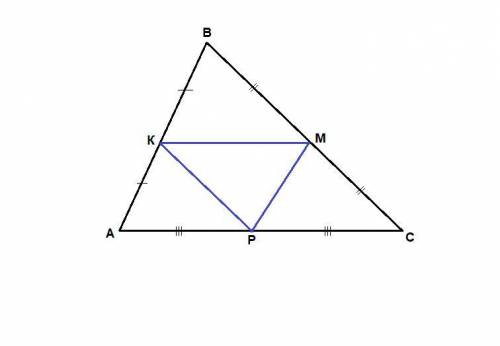
угол ACB с вершиной на окружности, опирающийся на диаметр является прямым = 90
угол CBA = 90 - CAB = 20